
5.函数的最大值和最小值: 一般地,在闭区间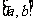 上连续的函数
上连续的函数 在
在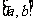 上必有最大值与最小值.
上必有最大值与最小值.
 利用导数研究多项式函数单调性的一般步骤:
利用导数研究多项式函数单调性的一般步骤:
 求
求 ;
;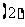 确定
确定 在
在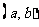 内符号;
内符号;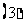 若
若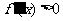 在
在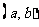 上恒成立,则
上恒成立,则 在
在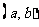 上是增函数;若
上是增函数;若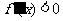 在
在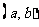 上恒成立,则
上恒成立,则 在
在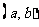 上是减函数
上是减函数
①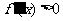

 为增函数(
为增函数(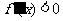

 为减函数).
为减函数).
② 在区间
在区间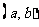 上是增函数
上是增函数
 ≥
≥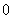 在
在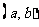 上恒成立;
上恒成立;
 在区间
在区间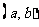 上为减函数
上为减函数
 ≤
≤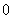 在
在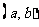 上恒成立.
上恒成立.
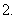 极大值: 一般地,设函数
极大值: 一般地,设函数 在点
在点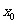 附近有定义,如果对
附近有定义,如果对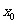 附近的所有的点,都有
附近的所有的点,都有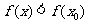 ,就说
,就说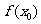 是函数
是函数 的一个极大值,记作
的一个极大值,记作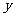 极大值
极大值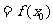 ,
,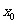 是极大值点.
是极大值点.
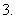 极小值:一般地,设函数
极小值:一般地,设函数 在
在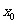 附近有定义,如果对
附近有定义,如果对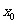 附近的所有的点,都有
附近的所有的点,都有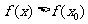 就说
就说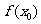 是函数
是函数 的一个极小值,记作
的一个极小值,记作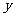 极小值
极小值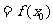 ,
,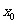 是极小值点。
是极小值点。
4.求可导函数 的极值的步骤:
的极值的步骤:
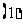 确定函数的定义区间,求导数
确定函数的定义区间,求导数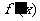
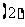 求方程
求方程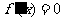 的根
的根
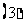 用函数的导数为
用函数的导数为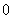 的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查
的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查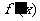 在方程根左右的值的符号,如果左正右负,那么
在方程根左右的值的符号,如果左正右负,那么 在这个根处取得极大值;如果左负右正,那么
在这个根处取得极大值;如果左负右正,那么 在这个根处取得极小值;如果左右不改变符号,那么
在这个根处取得极小值;如果左右不改变符号,那么 在这个根处无极值.如果函数在某些点处连续但不可导,也需要考虑这些点是否是极值点 .
在这个根处无极值.如果函数在某些点处连续但不可导,也需要考虑这些点是否是极值点 .
考纲点击: 理解可导函数的单调性与其导数的关系;
理解可导函数的单调性与其导数的关系; 了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);
了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号); 会求一些实际问题(一般指单峰函数)的最大值和最小值.
会求一些实际问题(一般指单峰函数)的最大值和最小值.
热点提示:
导数的应用已成为高考必考点,重点考查利用导数研究函数的单调性,求单调区间、极值、最值,以及利用导数解决生活中优化问题,可以与解析几何、不等式、平面向量等知识交汇命题。多以解答题出现,属中高档题。
5.已知函数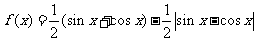 ,则
,则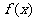 的值域是( )
的值域是( )
(A)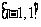 (B)
(B)  (C)
(C) 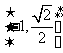 (D)
(D) 
4.  =
=
3.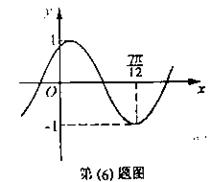 将函数
将函数 的图象按向量
的图象按向量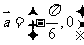 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
A.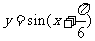 B.
B.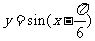
C.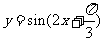 D.
D.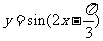
2.已知函数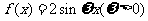 在区间
在区间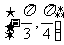 上的最小值是
上的最小值是 ,则
,则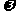 的最小值等于 ( B )
的最小值等于 ( B )
(A)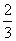 (B)
(B)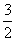 (C)2 (D)3
(C)2 (D)3
1。已知函数y =tan  在(-
在(-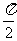 ,
,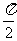 )内是减函数,则
)内是减函数,则
(A)0 < 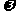 ≤ 1 (B)-1 ≤
≤ 1 (B)-1 ≤ 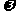 < 0 (C)
< 0 (C)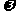 ≥ 1 (D)
≥ 1 (D)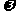 ≤ -1
≤ -1
12.已知f(x)=-4cos2x+4asinxcosx,将f(x)图象按向量=(-,2)平移后,图象关于直线x=对称.
(1)求实数a的值,并求f(x)取得最大值时x的集合;
(2)求f(x)的单调区间.
练习:
11.非等边三角形ABC的外接圆半径为2,最长的边BC=2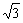 ,求sinB+sinC的取值范围.
,求sinB+sinC的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com