
5.曲线 在点
在点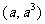
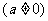 处的切线与
处的切线与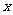 轴、直线
轴、直线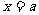 所围成的三角形的面积为
所围成的三角形的面积为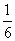 ,则
,则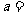 ▲
▲
4.已知二次函数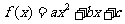 的导数为
的导数为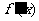 ,
,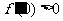 ,对于任意实数
,对于任意实数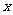 ,有
,有 ≥
≥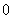 ,则
,则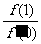 的最小值为 ▲
的最小值为 ▲
3.设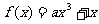 恰有三个单调区间,试确定
恰有三个单调区间,试确定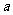 的取值范围,并求出这三个单调区间
的取值范围,并求出这三个单调区间
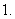 求满足条件的
求满足条件的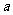 的范围:
的范围:
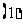 使
使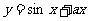 为
为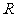 上增函数,则
上增函数,则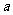 的范围是
的范围是
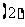 使
使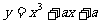 为
为 上增函数,则
上增函数,则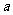 的范围是
的范围是
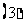 使
使 为
为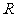 上增函数,则
上增函数,则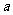 的范围是
的范围是
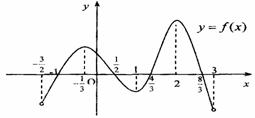
2.如图,是函数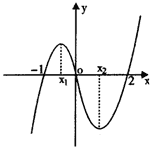
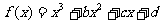 的大致图像,
的大致图像,
|
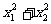 = ▲
= ▲ 热点考向一:导数的几何意义
例1.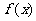 的导函数
的导函数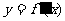 的图象如图所示,则
的图象如图所示,则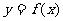 的图象最有可能的是( )
的图象最有可能的是( )
例2.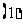 (
( 届云南平远一中五模)函数
届云南平远一中五模)函数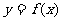 在定义域
在定义域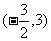 内可导,其图象如图所示,记
内可导,其图象如图所示,记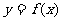 的导函数为
的导函数为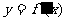 ,则不等式
,则不等式 的解集为
的解集为
(2)设 均是定义在
均是定义在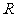 上的奇函数,当
上的奇函数,当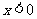 时,
时,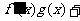
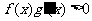 ,且
,且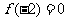 ,则不等式
,则不等式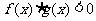 的解集是
的解集是
热点考向二:函数的极值,最值以及恒成立问题
例3:函数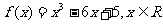 ,
,
(Ⅰ)求 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若关于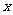 的方程
的方程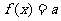 有
有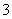 个不同实根,求实数
个不同实根,求实数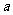 的取值范围.
的取值范围.
(Ⅲ)已知当 时,
时, ≥
≥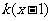 恒成立,求实数
恒成立,求实数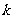 的取值范围.
的取值范围.
例4;已知定义在正实数集上的函数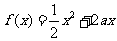 ,
,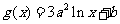 ,其中
,其中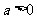 .设两曲线
.设两曲线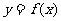 ,
,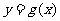 有公共点,且在该点处的切线相同.(Ⅰ)用
有公共点,且在该点处的切线相同.(Ⅰ)用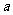 表示
表示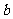 ,并求
,并求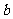 的最大值;(Ⅱ)求证:
的最大值;(Ⅱ)求证: ≥
≥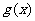 (
(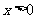 ).
).
热点考向三;生活中优化问题
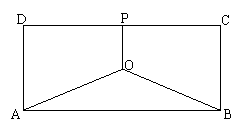
例5;某地有三家工厂,分别位于矩形ABCD的顶点A、B及CD的中点P处,已知AB=20km,BC=10km,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A、B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP,设排污管道的总长为ykm。
(1)按下列要求写出函数关系式:
①设∠BAO=θ(rad),将y表示成θ的函数关系式;
②设OP=x(km),将y表示成x的函数关系式;
(2)请你选用(1)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短。
2.(09湖南文)(本小题满分13分)
已知函数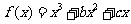 的导函数的图象关于直线x=2对称.
的导函数的图象关于直线x=2对称.
(Ⅰ)求b的值;
(Ⅱ)若 在
在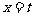 处取得最小值,记此极小值为
处取得最小值,记此极小值为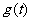 ,求
,求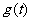 的定义域和值域。
的定义域和值域。
1.(09四川文)(本小题满分12分)
已知函数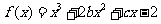 的图象在与
的图象在与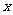 轴交点处的切线方程是
轴交点处的切线方程是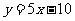 。
。
(I)求函数 的解析式;
的解析式;
(II)设函数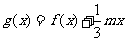 ,若
,若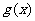 的极值存在,求实数
的极值存在,求实数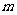 的取值范围以及函数
的取值范围以及函数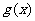 取得极值时对应的自变量
取得极值时对应的自变量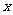 的值.
的值.
8.通过求导求函数不等式的基本思路是:以导函数和不等式为基础,单调性为主线,最(极值)为助手,从数形结合、分类讨论等多视角进行综合探索.
7.求参数范围的方法:①分离变量法;②构造(差)函数法.
6.利用导数求函数的最值步骤:
由上面函数 的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了.
的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了.
设函数 在
在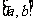 上连续,在
上连续,在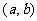 内可导,则求
内可导,则求 在
在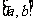 上的最大值与最小值的步骤如下:
上的最大值与最小值的步骤如下: 求
求 在
在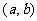 内的极值;
内的极值;
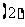 将
将 的各极值与
的各极值与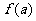 、
、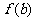 比较得出函数
比较得出函数 在
在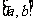 上的最值
上的最值 p
p
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com