
1课时.
3.教学疑点:正确理解等角定理中命题的条件:两个角的两边分别平行且这两个角的方向相同.
2.教学难点:等角定理证明的掌握及其应用.
1.教学重点:让学生掌握平行公理及其应用.
(二)能力训练点
1.利用联想的方法,掌握并应用由平面内引伸到空间中的平行公理.
2.充分利用构造的方法证明等角定理,为下一节两条异面直线所成的角的定义提供了可能性与唯一性.
3.通过本节课的学习,让学生认识到在平面几何中成立的结论或定理等,在用于非平面图形时,须先证明.
(一)知识教学点
1.公理4,即平行公理.
2.等角定理及推论.
16.设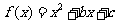 (
(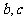 为常数),方程
为常数),方程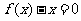 的两个实根为
的两个实根为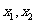 ,
,
且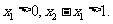 ①求证:
①求证: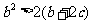 ②设
②设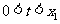 ,比较
,比较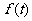 与
与 的大小
的大小
③若当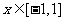 时对任意的
时对任意的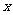 恒有
恒有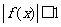 ,求证:
,求证: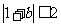
15.已知不等式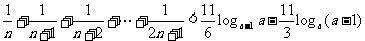 对于
对于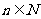 都成立,试求实数
都成立,试求实数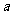 的取值范围。
的取值范围。
14.已知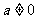 ,求证:
,求证: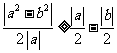
13.解关于 的不等式
的不等式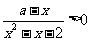
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com