

4.公式: 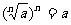 当n为奇数时
当n为奇数时 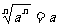
当n为偶数时 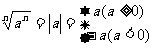
3.名称: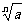 叫做根式 n叫做根指数 a叫做被开方数
叫做根式 n叫做根指数 a叫做被开方数
2.求法:当n为奇数时:正数的n次方根为正数,负数的n次方根为负数
记作: 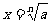 例(略)
例(略)
当n为偶数时,正数的n次方根有两个(互为相反数)
记作: 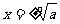
负数没有偶次方根
0的任何次方根为0
1.定义:若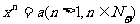 则x叫做a的n次方根。
则x叫做a的n次方根。
教材P.17习题二4、5、6、7、8.
(四)练习(P.14练习1、2.)
1.把一张长方形的纸对折两次,打开后如图1-44那样,说明为什么这些折痕是互相平行的?
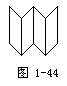
答:把一张长方形的纸对折两次,打开后得4个全等的矩形,每个矩形的竖边是互相平行的,再应用平行公理,可得知它们的折痕是互相平行的.
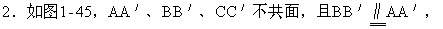
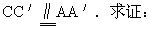
△ABC≌△A′B′C′.
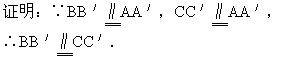
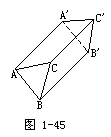
∴四边形BB′C′C是平行四边形.
∴BC=B′C′.
同理可证:AC=A′C′,AB=A′B′.
∴△ABC≌△A′B′C′.
(三)等角定理
师:平行公理不仅是今后论证平行问题的主要依据,也是证明等角定理的基础.
等角定理:如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等.
已知:∠BAC和∠B′A′C′的边AB∥A′B′,AC∥A′C′,并且方向相同.
求证:∠BAC=∠B′A′C′.
师分析:在平面内,这个结论我们已经证明成立了.在空间中,这个结论是否成立,还需通过证明.要证明两个角相等,常用的方法有:证明两个三角形全等或相似,则对应角相等;证明两直线平行,则同位角、内错角相等;证明平行四边形,则它的对角相等,等等.根据题意,我们只能证明两个三角形全等或相似,为此需要构造两个三角形,这也是本题证明的关键所在.
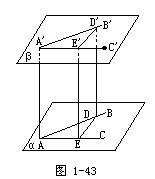
证明:对于∠BAC和∠B′A′C′都在同一平面内的情况,在平面几何中已经证明.下面我们证明两个角不在同一平面内的情况.
如图1-43,在AB、A′B′,AC、A′C′上分别取AD=A′D′、AE=A′E′,连结AA′、DD′、EE′,DE、D′E′.
∵AB∥A′B′, AD=A′D′,
∴AA′DD′是平行四边形.
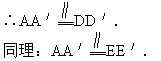
根据公理4,得:DD′∥EE′.
又可得:DD′=EE′
∴四边形EE′D′D是平行四边形.
∴ED=E′D′,可得:△ADE≌△A′D′E′.
∴∠BAC=∠B′A′C′.
师:若把上面两个角的两边反向延长,就得出下面的推论.
推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.
从上面定理的证明可以知道:平面里的定义、定理等,对于非平面图形,需要经过证明才能应用.
下面请同学们完成练习.
(二)平行公理
师:在平面几何中,如图1-40,若a∥b,c∥b,则a与c平行吗?
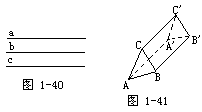
生:平行.
师:也就是说,在平面中,若两条直线a、c都和第三条直线b平行,则a∥c.这个命题在空间中是否成立呢?
师:实际上,在空间中,若a∥b,c∥b,则a∥c也成立.我们把这个结论作为一个公理,不必证明,可直接应用.
平行公理:平行于同一条直线的两条直线互相平行.
如图1-41,三棱镜的三条棱,若AA′∥BB′,CC′∥BB′,则有AA′∥CC′.
下面请同学们完成下列的例题,巩固应用平行公理.
例已知四边形ABCD是空间四边形(四个顶点不共面的图1-41四边形),E、H分别是边AB、AD的中点,F、G分别是边CB、CD

师分析:要证明四边形EFGH是梯形,即要证明四边形EFGH的一组对边平行,另一组对边不平行;或证明一组对边平行且不相等.具体用哪一种方法,我们来分析一下题意:E、H分别是边AB、AD的中



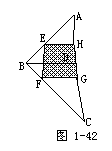
证明:如图1-42,连结BD.
∵EH是△ABD的中位线,



根据公理4,EH∥FG,
又∵FG>EH,
∴四边形EFGH是梯形.
(一)复习两条直线的位置关系(幻灯显示)
师:空间中两条直线的位置关系有哪几种?
生:三种:相交、平行、异面.异面直线是指不同在任何一个平面内的两条直线.相交直线和平行直线也称为共面直线.
师:异面直线的画法常用的有哪几种?
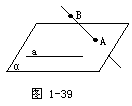
生:三种.如图1-38,a与b都是异面直线.
师:如何判定两条直线是异面直线?
生:(1)间接证法:根据定义,一般用反证法.
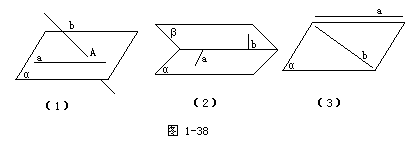
(2)直接证法:根据例题结论:过平面外一点与平面内一点的

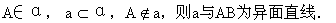
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com