
1.(2008-2009学年度潍坊市昌乐一中第一学期高三教学质量检测)(9分)某兴趣小组同学
共同设计了如图所示的多功能实验装置。该装置既可用于制取气体,又可用于验证物质
的性质。
(1)现有以下药品:锌粒、铜片、浓H2SO4、浓HNO3、蒸馏水、NaOH溶液。打开K1
关闭K2,可制取 气体。
(2)某同学用石灰石、醋酸、硅酸钠溶液等药品设计了另一实验。他的实验目的是
__________________________________________________;打开K2关闭K1,将A
中液体加入B中后,观察到的实验现象为___________________________________。
21.(12分)设数列 前
前 项和为
项和为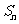 ,且
,且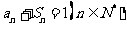
(1)若数列 满足
满足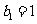 且
且 ,求数列
,求数列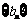 的通项公式。
的通项公式。
(2)(文)若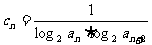 ,数列{
,数列{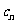 }的前
}的前 项和为
项和为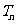 ,求证Tn<3/4
,求证Tn<3/4
(理)若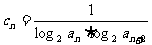 ,数列{
,数列{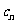 }的前
}的前 项和为
项和为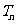 ,求
,求
解:(1)∵ ∴
∴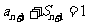
两式相减得: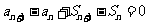 ∴
∴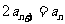
又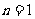 时,
时,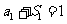 ∴
∴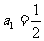
∴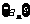 是首项为
是首项为 ,公差为
,公差为 的等差数列
的等差数列
∴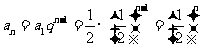
∵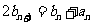 ∴
∴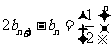
两边同乘以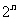 得:
得: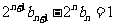
∴ 是首项为
是首项为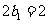 ,公差为
,公差为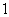 的等差数列
的等差数列
∴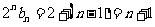 ∴
∴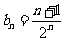
(2) 裂项法, =3/4
=3/4
22 (07眉山二诊)已知关于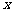 的方程
的方程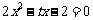 的两个根为
的两个根为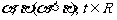 ,设函数
,设函数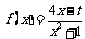 .
.
①
判断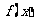 在
在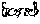 上的单调性;若
上的单调性;若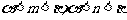 ,证明
,证明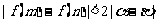 .
.
解答①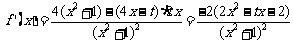 ....................3’
....................3’
由于当 时
时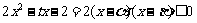 ,
,
所以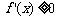 ,故
,故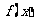 在
在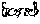 上是增函数.......................6’
上是增函数.......................6’
②当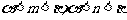 时,并由①得
时,并由①得
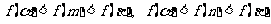 .................................7’
.................................7’
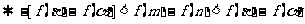
 ...............................................................................9’
...............................................................................9’
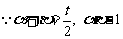
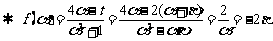 ................................11’
................................11’
同理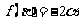 ............................................................................................................12’
............................................................................................................12’
于是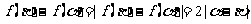
从而有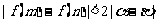 .........................................14’
.........................................14’
方法二、②当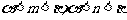 时,并由①得
时,并由①得
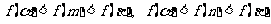
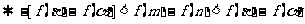


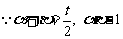 且
且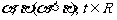

所以有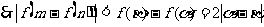
(文) 已知函数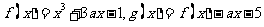 ,其中
,其中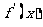 是的导函数
是的导函数
(Ⅰ)对满足 的一切
的一切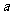 的值,都有
的值,都有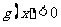 ,求实数
,求实数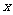 的取值范围;
的取值范围;
(Ⅱ)当实数a在什么范围内变化时,函数 的图象与直线
的图象与直线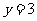 只有一个公共点
只有一个公共点
本小题主要考察函数的单调性、导数的应用、解不等式等基础知识,以及推理能力、运输能力和综合应用数学知识的能力。
解:(Ⅰ)由题意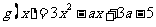 令
令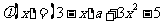 ,
,
对 ,恒有
,恒有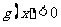 ,即
,即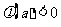
∴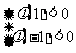 即
即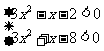 解得
解得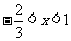
故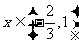 时,对满足
时,对满足 的一切
的一切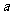 的值,都有
的值,都有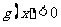
20. (南充市高2007届第二次高考适应性考试试题)已知向量 ,O是坐标原点,动点M满足:
,O是坐标原点,动点M满足: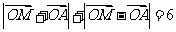 ①求点M的轨迹C的方程
①求点M的轨迹C的方程
②是否存在直线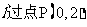 与轨迹C交于A,B两点,且以AB为直径的圆过原点?若存在,求出直线
与轨迹C交于A,B两点,且以AB为直径的圆过原点?若存在,求出直线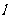 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。

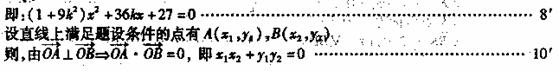

19. 解:作MN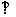 CF于N,连结EN,由三垂线定理知EN
CF于N,连结EN,由三垂线定理知EN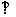 CF
CF
 为二面角E-FC-D的平面角
为二面角E-FC-D的平面角
MN=1,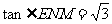 故二面角E-FC-D为
故二面角E-FC-D为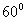
(2)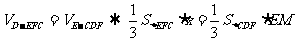 (x为D到面EFC的距离)
(x为D到面EFC的距离)
故D到面EFC的距离为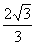 。
。
19.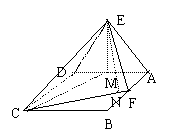 如图,边长为2的正三角形ADE垂直于矩形ABCD所在平面,F是AB的中点,EC和平面ABCD成45
如图,边长为2的正三角形ADE垂直于矩形ABCD所在平面,F是AB的中点,EC和平面ABCD成45 角.(1) 求二面角E-FC-D的大小;(2) 求D到平面EFC的距离.(12分)
角.(1) 求二面角E-FC-D的大小;(2) 求D到平面EFC的距离.(12分)
17函数f(x)=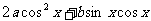 满足
满足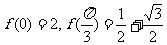
(1)若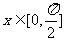 ,求
,求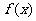 的最大值和最小值;(2)若
的最大值和最小值;(2)若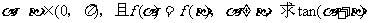
解:(1)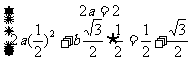
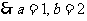
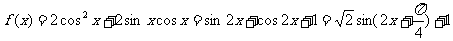
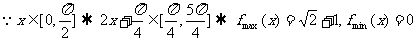
(2)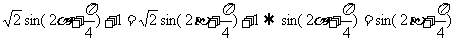
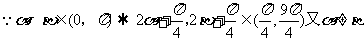
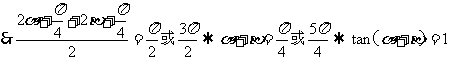
18. (2007届四川成都四中)某中学高三(1)班的一个研究性学习小组在网上查知,某珍稀植物种子在一定条件下发芽成功的概率为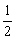 ,该研究性学习小组又分成两个小组进行验证性实验.
,该研究性学习小组又分成两个小组进行验证性实验.
(Ⅰ)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验至少有3次成功的概率;
(Ⅱ)(文)第二小组做了若干次发芽实验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则将继续进行下次实验,直到种子发芽成功为止,但发芽实验的次数最多不超过5次的概率
(理)第二小组做了若干次发芽实验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则将继续进行下次实验,直到种子发芽成功为止,但发芽实验的次数最多不超过5次,求第二小组所做种子发芽实验的次数ξ的概率分布列和期望.
解:(Ⅰ)至少有3次发芽成功,即有3次、4次、5次发芽成功,
∴所求概率P=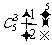 +
+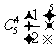 +
+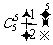 =
=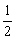 . …………………6分
. …………………6分
(Ⅱ)(文)
|
ξ |
1 |
2 |
3 |
4 |
5 |
|
P |
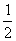 |
 |
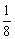 |
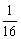 |
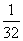 |
P=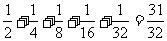
(理)ξ的分布列为
|
…………………9分
Eξ=1×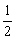 +2×
+2× +3×
+3×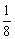 +4×
+4×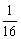 +5×
+5×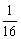 =
=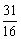 . ………………12分
. ………………12分
16、(江西省五校2008届高三开学联考)设{x}表示离x最近的整数,即若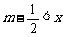 ≤
≤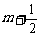 (m∈Z),则{x} = m.给出下列关于函数
(m∈Z),则{x} = m.给出下列关于函数 的四个命题:
①函数
的四个命题:
①函数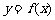 的定义域是R,值域是[0,
的定义域是R,值域是[0,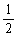 ];
②函数
];
②函数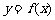 的图像关于直线
的图像关于直线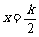 (k∈Z)对称;
③函数
(k∈Z)对称;
③函数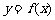 是周期函数,最小正周期是1;
④函数
是周期函数,最小正周期是1;
④函数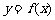 是连续函数,但不可导.
其中真命题是
.
是连续函数,但不可导.
其中真命题是
.
答案:①②③④
15、已知关于x不等式的不等式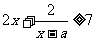 在
在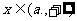 上恒成立,则实数a的最小值为
上恒成立,则实数a的最小值为 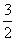 .
.
13遵义四中2008年高三联考)设向量a =(-1,2),b =(2,-1),则(a - b)·(a + b)等于0。
14、等差数列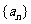 中,
中,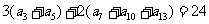 ,则此数列前13项和是26
,则此数列前13项和是26
12. 已知命题P:不等式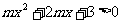 在R上恒成立;命题q:函数
在R上恒成立;命题q:函数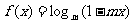 在区间[0,2]是增函数.若“P或q”为真命题,“P 且q”为假命题.则m的取值范围是
在区间[0,2]是增函数.若“P或q”为真命题,“P 且q”为假命题.则m的取值范围是
A、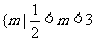 }
B、
}
B、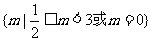
C、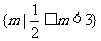 D、
D、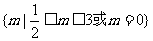
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com