
4、数列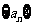 满足
满足 ,
,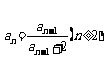 ,则使得
,则使得 的最大正整数k为
的最大正整数k为
A.5 B.7 C.8 D.10
3、已知等比数列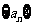 ,若
,若 +
+ =20,
=20, +
+ =80,则
=80,则 +
+ 等于
等于
A.480 B.320 C.240 D.120
2、某船开始看见灯塔在南偏东30 方向,后来船沿南偏东60
方向,后来船沿南偏东60 的方向航行45km后,看见灯塔在正西方向,则这时船与灯塔的距离是
的方向航行45km后,看见灯塔在正西方向,则这时船与灯塔的距离是
A.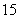 km B.
km B. km C.
km C.
 km D.
km D. km
km
1、已知等差数列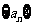 中,前n项和为S
中,前n项和为S ,若
,若 +
+ =6,则S11=
=6,则S11=
A.12 B.33 C.66 D.99
(三)、不等式的综合应用
7.(1)下列结论正确的是 ( )
A.当 B.
B.
C. 的最小值为2 D.当
的最小值为2 D.当 无最大值
无最大值
(2)若x>2,则 的最小值是______若
的最小值是______若 ,则
,则 的最小值为_________.
的最小值为_________.
(3)若 对任意正实数
对任意正实数 恒成立,则正实数
恒成立,则正实数 的最小值为______
的最小值为______
(4)若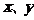 是正数,则
是正数,则 的最小值是_______________.
的最小值是_______________.
(5)若 且
且 ,则
,则 的最小值为________.
的最小值为________.
8.已知 是实数,函数
是实数,函数 ,如果函数
,如果函数 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围.
练习:1.不等式组 的解集为 ( )
的解集为 ( )
(0, ); (B) (
); (B) ( ,2); (C) (
,2); (C) ( ,4); (D) (2,4)。
,4); (D) (2,4)。
2.不等式 的解集为
的解集为
3.若关于 的不等式
的不等式 ≤
≤ +4的解集是M,则对任意实常数
+4的解集是M,则对任意实常数 ,总有( )
,总有( )
(A)2∈M,0∈M; (B)2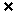 M,0
M,0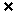 M;
(C)2∈M,0
M;
(C)2∈M,0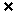 M;
(D)2
M;
(D)2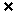 M,0∈M.
M,0∈M.
4.
“a>b>c”是“ab<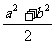 ”的 ( )
”的 ( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不允分也不必要条件
5.对a,b R,记max|a,b|=
R,记max|a,b|= 函数f(x)=max||x+1|,|x-2||(x
函数f(x)=max||x+1|,|x-2||(x R)的最小值是 .
R)的最小值是 .
6.设f(x)= 
 则不等式f(x)>2的解集为 ( )
则不等式f(x)>2的解集为 ( )
(A)(1,2) (3,+∞) (B)(
(3,+∞) (B)( ,+∞) (C)(1,2)
,+∞) (C)(1,2) (
( +∞)(D)(1,2)
+∞)(D)(1,2)
7. 若不等式x2+ax+1³0对于一切xÎ(0, )成立,则a的取值是( )
)成立,则a的取值是( )
A.0
B. –2 C.- D.-3
D.-3
(二)、解下列不等式:
1.已知函数 在区间
在区间 内连续,且
内连续,且 .
.
(1)求实数 和
和 的值;
(2)解不等式
的值;
(2)解不等式 .
.
2.(1)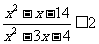 (2)
(2)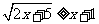
2.(1) (2)
(2)
3. (1) (2)
(2)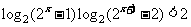
4. (1) (2)
(2) (3)
(3)
5.若 ,则
,则 的取值范围是 ( )
的取值范围是 ( )
A. B.
B. C.
C.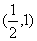 D.
D.
(一)基本性质
1. 若 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
(A) . (B)
. (B) . (C)
. (C) .(D)
.(D)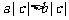 .
.
2.设a、b、c是互不相等的正数,则下列等式中不恒成立的是
(A) (B)
(B)
(C) (D)
(D)
3.若a>0,b>0,则不等式-b< <a等价于(
)
<a等价于(
)
A. <x<0或0<x<
<x<0或0<x< B.-
B.- <x<
<x< C.x<-
C.x<- 或x>
或x> D.x<
D.x< 或x>
或x>
4.在下列四个函数中,满足性质:“对于区间 上的任意
上的任意 ,
, 恒成立”的只有 ( )
恒成立”的只有 ( )
(A) (B)
(B) (C)
(C) (D)
(D)
5. ,下列不等式一定成立的是( )
,下列不等式一定成立的是( )
(A) (B)
(B)
(C)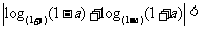

(D)

若 ,则
,则 (当且仅当
(当且仅当 时取等号)
时取等号)
基本变形:① ;
; ;
;
②若 ,则
,则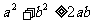 ,
,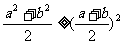
基本应用:①放缩,变形;
②求函数最值:注意:①一正二定三取等;②积定和小,和定积大。
当 (常数),当且仅当
时,
;
(常数),当且仅当
时,
;
当 (常数),当且仅当
时,
;
(常数),当且仅当
时,
;
常用的方法为:拆、凑、平方;
五:例题:
(1)一元一次不等式:
Ⅰ、 :⑴若
:⑴若 ,则
;⑵若
,则
;⑵若 ,则
;
,则
;
Ⅱ、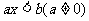 :⑴若
:⑴若 ,则
;⑵若
,则
;⑵若 ,则
;
,则
;
(2)一元二次不等式:
一元二次不等式二次项系数小于零的,同解变形为二次项系数大于零;注:要对 进行讨论:
进行讨论:
(3)绝对值不等式:若 ,则
,则 ;
;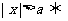 ;
;
注意:(1).几何意义: :
;
:
;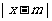 :
:
(2)解有关绝对值的问题,考虑去绝对值,去绝对值的方法有:
⑴对绝对值内的部分按大于、等于、小于零进行讨论去绝对值;①若 则
则 ;②若
;②若 则
则 ;③若
;③若 则
则 ;(2).通过两边平方去绝对值;需要注意的是不等号两边为非负值。(3).含有多个绝对值符号的不等式可用“按零点分区间讨论”的方法来解。
;(2).通过两边平方去绝对值;需要注意的是不等号两边为非负值。(3).含有多个绝对值符号的不等式可用“按零点分区间讨论”的方法来解。
(4)分式不等式的解法:通解变形为整式不等式;
⑴ ;⑵
;⑵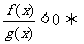 ⑶
⑶ ⑷
⑷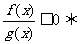 _______
_______
(5)解含有参数的不等式:
解含参数的不等式时,首先应注意考察是否需要进行分类讨论.如果遇到下述情况则一般需要讨论:
①不等式两端乘除一个含参数的式子时,则需讨论这个式子的正、负、零性.
②在求解过程中,需要使用指数函数、对数函数的单调性时,则需对它们的底数进行讨论.
③在解含有字母的一元二次不等式时,需要考虑相应的二次函数的开口方向,对应的一元二次方程根的状况(有时要分析△),比较两个根的大小,设根为 (或更多)但含参数,要分
(或更多)但含参数,要分 、
、 、
、 讨论。
讨论。
(1)设 ,则
,则 (当且仅当
时取等号)
(当且仅当
时取等号)
(2) (当且仅当
时取等号);
(当且仅当
时取等号); (当且仅当
时取等号)
(当且仅当
时取等号)
(3) ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com