解：∵ 　　∴函数的定义域为 R

且 　f (x) + f (-x)

∴f (x) = - f (-x) 　　∴f (x) 为奇函数

　　 注：判断函数奇偶性的又一途径：f (x) + f (-x) = 0　 　为奇函数

　　　　　　　　　　　　　　　　　 　f (x) + f (-x) = 2 f (x) 　为偶函数

4．若 x > 0时，f (x) = x² - 2x , 　则 x < 0 时，f (x) = - x² - 2x 。

　　 其中正确的序号是： ① ② ④ 　

3．若 f (x) 在 [1, 上为增函数，则 f (x) 在 上为减函数。

2．若 f (x) 在 [0, 上有最小值 -1，则 f (x) 在上有最大值1。

1．f (0) = 0

　 解：f (x) 定义域：[0,

又∵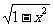≥0 　∴只要 1 - x²≥0 即 x²≤1 　∴ - 1 ≤ x ≤ 1

当 x Î [ 0, 1] 时,　 u =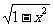关于 x 递增, f (u)关于 x 递减 　

∴单调区间为 [-1，0]

　 证：任取 x₁, x Î R 且 x₁ < x₂　

∵g (x) 在R上是增函数　 　∴g (x₁) <g (x₂)

又∵f (x) 在R上是增函数　 ∴f [g (x₁)] < f [g (x₂)]

而且 x₁ < x₂∴ f [g (x)] 在R上是增函数

同理可以推广：

若 f (x)、g (x) 均是R上的减函数，则 f [g (x)] 是R上的增函数

　 　若 f (x)、g (x) 是R上的一增、一减函数，则 f [g (x)] 是R上的减函数

第3题是两个函数之乘积, 尤其后者要利用幂指数概念

应突出“二次函数”，再结合图象分析

　　　　　　　　　 　而且：∵x₁, x₂中至少有一个不为0, ∴……

　　　　　　　　　 　反之，倘若 x_1, x₂全为0　 x² + x₁x₂ + x₂ = 0