
7.程序框图如下:

如果上述程序运行的结果为S=132,那么判断框中应填入( )
A. B.
B. C.
C. D.
D.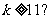
6.将函数 的图象先向左平移
的图象先向左平移 ,然后将所得图象上所有的点的横坐标变为原来的
,然后将所得图象上所有的点的横坐标变为原来的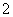 倍(纵坐标不变),则所得到的图象对应的函数解析式为( ).
倍(纵坐标不变),则所得到的图象对应的函数解析式为( ).
A. B.
B. C.
C. D.
D.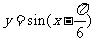
5. 下列函数为奇函数的是( ).
 .
. B.
B.
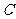 .
.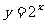
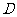 .
.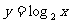
4.原命题:“设 、
、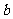 、
、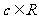 ,若
,若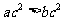 则
则 ”的逆命题、否命题、逆否命题真命题共有:( )A.0个 B.1个 C.2个 D.3个
”的逆命题、否命题、逆否命题真命题共有:( )A.0个 B.1个 C.2个 D.3个
3.如果点P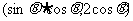 位于第三象限,那么角
位于第三象限,那么角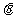 所在的象限是:( )
所在的象限是:( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.化简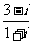 ( )
( )
A.1+2i B. 1–2i C.2+i D.2–i
1.设集合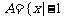 ≤x≤2},B={x|0≤x≤4},则A∩B=( )
≤x≤2},B={x|0≤x≤4},则A∩B=( )
A.[0,2] B.[1,2] C.[0,4] D.[1,4]
18.(10分) 已知 在区间
在区间 上是增函数。
上是增函数。
(Ⅰ)求实数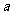 的值所组成的集合
的值所组成的集合 ;
;
(Ⅱ)设关于 的方程
的方程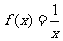 的两个根为
的两个根为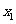 、
、 ,若对任意
,若对任意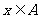 及
及 ,不等式
,不等式
 恒成立,求
恒成立,求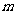 的取值范围.
的取值范围.
17.(本小题满分10分) 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
16. 甲、乙两地相距S(千米),汽车从甲地匀速行驶到乙地,速度最大不得超过c(千米/小时).已知汽车每小时的运输成本(元)由可变部分与固定部分组成.可变部分与速度v(千米/小时)的平方成正比,且比例系数为正常数b;固定部分为a元.
(1) 试将全程运输成本Y(元)表示成速度V(千米/小时)的函数.
(2) 为使全程运输成本最省,汽车应以多大速度行驶?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com