12、(08宁波)如图，□ABCD中，AB＝4，点D的坐标是(0，8)，以点C为顶点的抛物线y＝ax²+bx+c经过x轴上的点A、B．

(1)求点A、B、C的坐标．

(2)若抛物线向上平移后恰好经过点D，求平移后抛物线的解析式．

11、(河北)某跳水运动员进行10米跳台跳水训练,身体(将运动员看成一点)在空中运动的路线是如图所示坐标系经过原点O的抛物线(图中标出的数据为已知数据).在跳某个规定动作时,正常情况下,该运动员在空中最高处距水面10米,入水处距池边4米.同时,运动员在距水面高度5米以前,必须完成规定的翻腾、打开动作,并调整好入水姿势,否则就会失误.

(1)求这条抛物线的关系式;

(2)某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时距池边的水平距离为3米,问此次跳水会不会失误? 通过计算说明理由.

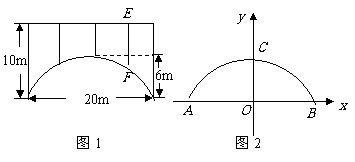
10、(兰州08)一座拱桥的轮廓是抛物线型(如图10-1所示)，拱高6m，跨度20m，相邻两支柱间的距离均为5m．

(1)将抛物线放在所给的直角坐标系中(如图10-2所示)，求抛物线的解析式；

(2)求支柱的长度；

(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带)，其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)？请说明你的理由．

9、(05武汉)如图，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为8m，宽AB为2m，以BC所在的直线为x轴，线段BC的中垂线为y轴，建立平面直角坐标系。y轴是抛物线的对称轴，顶点E到坐标原点O的距离为6m。

(1)求抛物线的解析式；

(2)如果该隧道内设双行道，现有一辆货运卡车高4.2m，宽2.4米，这辆货运卡车能否通过该隧道？通过计算说明你的结论。

8、(河北)如图，这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图，横断面的地平线为x轴，横断面的对称轴为y轴．桥拱的DGD′部分为一段抛物线，顶点G的高度为8米，AD和A′D′的两侧高为5.5米的支柱，OA和OA′为两个方向的汽车通行区，宽都为15米，线段CD和C′D′为两段对称的上桥斜坡，其坡度为1∶4．

(1)求桥拱DGD′所在抛物线的解析式及CC′的长；

(2)BE和B′E′为支撑斜坡的立柱，其高都为4米，相应的AB和A′B′为两个方向的行人及非机动车通行区．试求AB和A′B′的宽；

(3)按规定，汽车通过该桥下时，载货最高处和桥拱之间的距离不得小于0.4米．今有一大型运货汽车，装载某大型设备后，其宽为4米，车载大型设备的顶部与地面的距离均为7米．它能否从OA(或OA′)区域安全通过？请说明理由．

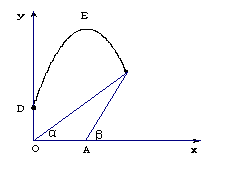
7、如图，这是某次运动会开幕式上点燃火炬时在平面直角坐标系中的示意图，在地面有O、A两个观测点，分别测得目标点火炬C的仰角为α、β，OA＝2米，tanα=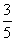,tanβ=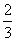,位于点O正上方2米处的D点发射装置，可以向目标C发射一个火球点燃火炬，该火球运行的轨迹为一抛物线，当火球运行到距地面最大高度20米时，相应的水平距离为12米，(图中E点)

(1)求火球运行轨迹的抛物线对应的函数解析式;

(2)说明按(1)中轨迹运行的火球能否点燃目标C.

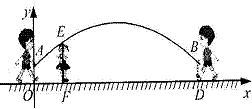
6、(金华08)跳绳时，绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米，到地 面的距离AO和BD均为O. 9米，身高为1.4米的小丽站在距点O的水平距

离为1米的点F处，绳子甩到最高处时刚好通过她的头顶点E。以点O为原点建立如图所示

的平面直角坐标系，设此抛物线的解析式为y=ax²+bx+0.9.

(1)求该抛物线的解析式；

(2)如果小华站在OD之间，且离点O的距离为3米，当绳子甩到最高处时刚好通过他的头顶，

请你算出小华的身高；

(3)如果身高为1.4米的小丽站在OD之间，且离点O的距离为t米，绳子甩到最高处时超过她的

头顶，请结合图像，写出t取值范围　　 。

5、(08桂林)桂林红桥位于桃花江上，是桂林两江四湖的一道亮丽的风景线，该桥的部分横截面如图所示，上方可看作是一个经过A、C、B三点的抛物线，以桥面的水平线为X轴，经过抛物线的顶点C与X轴垂直的直线为Y轴，建立直角坐标系，已知此桥垂直于桥面的相邻两柱之间距离为2米(图中用线段AD、CO、BE等表示桥柱)CO＝1米，FG＝2米

(1)　 求经过A、B、C三点的抛物线的解析式。

(2)　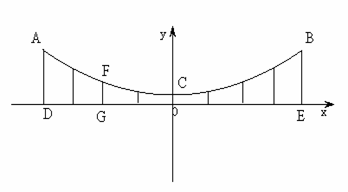 求柱子AD的高度。

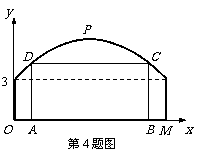
4、(08佛山)如图，某隧道横截面的上下轮廓线分别由抛物线对称的一部分和矩形的一部

分构成，最大高度为6米，底部宽度为12米. 现以O点为原点，OM所在直线为x轴建立

直角坐标系.

(1) 直接写出点M及抛物线顶点P的坐标；

(2) 求出这条抛物线的函数解析式；

(3) 若要搭建一个矩形“支撑架”AD- DC- CB，使C、D点在抛物线上，A、B点在地面OM上，则这个“支撑架”总长的最大值是多少？

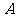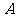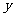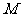3、(08长春)如图，足球场上守门员在处开出一高球，球从离地面1米的处飞出(在轴上)，运动员乙在距点6米的处发现球在自己头的正上方达到最高点，距地面约4米高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．

(1)求足球开始飞出到第一次落地时，该抛物线的表达式．

(2)足球第一次落地点距守门员多少米？(取)

(3)运动员乙要抢到第二个落点，他应再向前跑多少米？

(取)