
32、(长春07)如图①,在Rt△ABC中,∠C=90°,边BC的长为20cm,边AC的长为hcm,在此三角形内有一个矩形CFED,点D、E、F分别在AC、AB、BC上,设AD的长为xcm,矩形CFED的面积为y(单位:cm2).
(1)当h等于30时,求y与x的函数关系式(不要求写出自变量x的取值范围);
(2)在(1)的条件下,矩形CFED的面积能否为180cm2?请说明理由;
(3)若y与x的函数图象如图②所示,求此时h的值.
(参考公式:二次函数y=ax2+bx+c,当 时,y最大(小)值=
时,y最大(小)值= .)
.)

31、(08聊城)如图,把一张长10cm,宽8cm的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)要使长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
(2)你感到折合而成的长方体盒子的侧面积会不会有更大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由;
(3)如果把矩形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的矩形,然后折合成一个有盖的长方体盒子,是否有侧面积最大的情况;如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由.

30、(08邵阳)如图, 、
、 是竖立在公路两侧,且架设了跨过公路的高压电线的电杆,
是竖立在公路两侧,且架设了跨过公路的高压电线的电杆, 米.现在点
米.现在点 处观测电杆
处观测电杆 的视角为
的视角为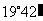 ,视线
,视线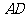 与
与 的夹角为
的夹角为
 .以点
.以点 为坐标原点,向右的水平方向为
为坐标原点,向右的水平方向为 轴的正方向,建立平面直角坐标系.
轴的正方向,建立平面直角坐标系.
(1)求电杆 、
、 之间的距离和点
之间的距离和点 的坐标;
的坐标;
(2)在今年年初的冰雪灾害中,高压电线由于结冰下垂近似成抛物线 (
( 为常数).在通电情况,高压电线周围12米内为非安全区域.请问3.2米高的车辆从高压电线下方通过时,是否有危险,并说明理由.
为常数).在通电情况,高压电线周围12米内为非安全区域.请问3.2米高的车辆从高压电线下方通过时,是否有危险,并说明理由.
温馨提示:[抛物线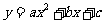 (
( )的顶点坐标
)的顶点坐标 .
.

 .]
.]
29、(扬州07)连接上海市区到浦东国际机场的磁悬浮轨道全长约为 ,列车走完全程包含启动加速、匀速运行、制动减速三个阶段.已知磁悬浮列车从启动加速到稳定匀速动行共需
,列车走完全程包含启动加速、匀速运行、制动减速三个阶段.已知磁悬浮列车从启动加速到稳定匀速动行共需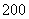 秒,在这段时间内记录下下列数据:
秒,在这段时间内记录下下列数据:
时间 (秒) (秒) |
0 |
50 |
100 |
150 |
200 |
速度 (米/秒) (米/秒) |
0 |
30 |
60 |
90 |
120 |
路程 (米) (米) |
0 |
750 |
3000 |
6750 |
12000 |
(1)请你在一次函数、二次函数和反比例函数中选择合适的函数来分别表示在加速阶段( )速度
)速度 与时间
与时间 的函数关系、路程
的函数关系、路程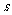 与时间
与时间 的函数关系.
的函数关系.
(2)最新研究表明,此种列车的稳定运行速度可达180米/秒,为了检测稳定运行时各项指标,在列车达到这一速度后至少要运行100秒,才能收集全相关数据.若在加速过程中路程、速度随时间的变化关系仍然满足(1)中的函数关系式,并且制动减速所需路程与启动加速的路程相同.根据以上要求,至少还要再建多长轨道就能满足试验检测要求?
(3)若减速过程与加速过程完全相反.根据对问题(2)的研究,直接写出列车在试验检测过程中从启动到停车这段时间内,列车离开起点的距离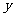 (米)与时间
(米)与时间 (秒)的函数关系式(不需要写出过程)
(秒)的函数关系式(不需要写出过程)
28、(08扬州)红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
|
时间t(天) |
1 |
3 |
5 |
10 |
36 |
… |
|
日销售量m(件) |
94 |
90 |
86 |
76 |
24 |
… |
未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为 (
(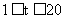 且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为
且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为 (
( 且t为整数)。下面我们就来研究销售这种商品的有关问题:
且t为整数)。下面我们就来研究销售这种商品的有关问题:
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程。公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围。
27、(08河北)研究所对某种新型产品的产销情况进行了研究,为投资商在甲、乙两地生产并销售该产品提供了如下成果:第一年的年产量为 (吨)时,所需的全部费用
(吨)时,所需的全部费用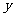 (万元)与
(万元)与 满足关系式
满足关系式 ,投入市场后当年能全部售出,且在甲、乙两地每吨的售价
,投入市场后当年能全部售出,且在甲、乙两地每吨的售价 ,
, (万元)均与
(万元)均与 满足一次函数关系.(注:年利润=年销售额-全部费用)
满足一次函数关系.(注:年利润=年销售额-全部费用)
(1)成果表明,在甲地生产并销售 吨时,
吨时, ,请你用含
,请你用含 的代数式表示甲地当年的年销售额,并求年利润
的代数式表示甲地当年的年销售额,并求年利润 (万元)与
(万元)与 之间的函数关系式;
之间的函数关系式;
(2)成果表明,在乙地生产并销售 吨时,
吨时,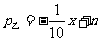 (
( 为常数),且在乙地当年的最大年利润为35万元.试确定
为常数),且在乙地当年的最大年利润为35万元.试确定 的值;
的值;
(3)受资金、生产能力等多种因素的影响,某投资商计划第一年生产并销售该产品18吨,根据(1),(2)中的结果,请你通过计算帮他决策,选择在甲地还是乙地产销才能获得较大的年利润?
参考公式:抛物线 的顶点坐标是
的顶点坐标是 .
.
26、(05潍坊)某工厂生产的某种产品按质量分为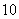 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产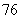 件,每件利润
件,每件利润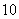 元,每提高一个档次,利润每件增加
元,每提高一个档次,利润每件增加 元.
元.
(1)每件利润为 元时,此产品质量在第几档次?
元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天产量减少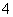 件.若生产第
件.若生产第 档的产品一天的总利润为
档的产品一天的总利润为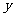 元(其中
元(其中 为正整数,且
为正整数,且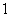 ≤
≤ ≤
≤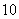 ),求出
),求出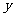 关于
关于 的函数关系式;若生产某档次产品一天的总利润为
的函数关系式;若生产某档次产品一天的总利润为 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品?
25、(03河北)某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元进行批量生产。已知生产每件产品的成本为40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为 元,年销售量为
元,年销售量为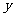 万件,年获利(年获利=年销售额-生产成本-投资)
万件,年获利(年获利=年销售额-生产成本-投资) 万元。
万元。
(1)试写出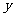 与
与 之间的函数关系式;(不必写出
之间的函数关系式;(不必写出 的取值范围)
的取值范围)
(2)试写出 与
与 之间的函数关系式;(不必写出
之间的函数关系式;(不必写出 的取值范围)
的取值范围)
(3)计算销售单价为160元时的年获利,并说明同样的年获利,销售单价还可以定为多少元?相应的年销售量分别为多少万件?
(4)公司计划:在第一年按年获利最大确定的销售单价进行销售,第二年年获利不低于1130万元。请你借助函数的大致图象说明,第二年的销售单价 (元)应确定在什么范围内?
(元)应确定在什么范围内?
24、(河北05)某机械租赁公司有同一型号的机械设备40套。经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出。在此基础上,当每套设备的月租金每提高10元时,这种设备就少租出一套,且没租出的一套设备每月需支出费用(维护费、管理费等)20元。设每套设备的月租金为x(元),租赁公司出租该型号设备的月收益(收益=租金收入-支出费用)为y(元)。
(1)用含x的代数式表示未出租的设备数(套)以及所有未出租设备(套)的支出费
(2)求y与x之间的二次函数关系式;
(3)当月租金分别为300元和350元式,租赁公司的月收益分别是多少元?此时应该出租多少套机械设备?请你简要说明理由;
(4)请把(2)中所求出的二次函数配方成 的形式,并据此说明:当x为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?
的形式,并据此说明:当x为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?
23、(06河北)利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7. 5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com