3.已知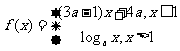是上的减函数，那么的取值范围是　　　　

2.已知f(x)为R上的减函数，则满足f(|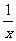|)<f(1)的实数x的取值范围是_____________

1.函数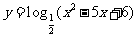的单调增区间为 　_____________

5．奇函数在其对称区间上的单调性　　　 ，偶函数在其对称区间上的单调性　　　　　 .

[基础过关]

1 下列函数中，在区间(0，2)上递增的有______________

①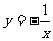　　　 ②y=-x　　　 ③y=|x-1|　　　 ④y=

2　　　　 函数的递减区间为_______________

3　　　　 已知函数在区间(-∞，4]上是减函数，则a的取值范围为___________________

4　　　　 已知f(x)是定义在R上的偶函数，且在[0,+∞]上是增函数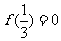，，则不等式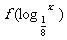的解集为_____________

　[典型例析]

(A)例1　 求证：函数在区间(-∞，0)上是单调增函数。

变式训练1：判断函数在区间(0,+∞)上单调性情况。在区间(-∞，0)上呢？

思考：讨论函数f(x)=x+(a＞0)的单调性.

(B)例2　 设函数，求a的取值范围，使函数f(x)在区间[-2，+∞)上是单调增函数。

(C)例3已知定义在区间(0，+∞)上的函数f(x)满足f(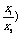=f(x₁)-f(x₂)，且当x＞1时，

f(x)＜0.

(1)求f(1)的值；

(2)判断f(x)的单调性；

(3)若f(3)=-1,解不等式f(|x|)＜-2.

小结：

[当堂检测]

4．复合函数y＝f [g(x)]是定义在M上的函数，若f (x)与g(x)的单调相同，则f [g(x)]为　　　　 ，若f (x), g(x)的单调性相反，则f [g(x)]为　　　　 .

3．互为反函数的两个函数有　　　　 的单调性；

2．若f (x)为增(减)函数，则－f (x)为　　　　　 ；

1．若f (x), g(x)均为增(减)函数，则f (x)+g(x)　　　　 函数；

2．判断单调性的方法：

(1) 定义法，其步骤为：①　　　 ；②　　　 ；③　　　 .

(2) 导数法，若函数y＝f (x)在定义域内的某个区间上可导，①若　　　　　　　 ，则f (x)在这个区间上是增函数；②若　　　　　　 ，则f (x)在这个区间上是减函数.

1．定义：如果函数y＝f (x)对于属于定义域I内某个区间上的任意两个自变量的值x_1、、x₂，当x_1、<x₂时，①都有　　　　 ，则称f (x)在这个区间上是增函数，而这个区间称函数的一个　　　　 　　　；②都有　　　　　　 ，则称f (x)在这个区间上是减函数，而这个区间称函数的一个　　　　　　 .

若函数f(x)在整个定义域l内只有唯一的一个单调区间，则f(x)称为　　　　 .