4．已知等腰三角形的一个底角等于30°，则这个等腰三角形的顶角等于

A、150°　　　　　 B、120°　　　　　 C、75°　　　　　　 D、30°

3．如图1，在△ABC中，D、E分别是AB、AC边的中点，

BC=16，则DE等于

A、5　　　　　 B、7　　　　　 C、8　　　　 D、12　　　 　　　图1

2．关于x的方程ax²–3x+2=0是一元二次方程，则

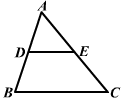A、a＞0　　 B、a≠0　　　 C、a＝1　　 D、a≥0

1．在△RtABC中，∠C=90°，∠A=60°，则tanA=

A、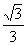　　　　　 B、　　　　　 C、　　　 D、

25、如图，在平面直角坐标系中有一直角梯形OABC，∠AOC=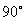，AB∥OC，OC在x轴上，过A、B、C三点的抛物线表达式为

(1)　　　 求A、B、C三点的坐标

(2)　　　 如果在梯形OABC内有一矩形MNPQ，使M在y轴上，N在BC边上，P在OC边上，当MN为多少时，矩形MNPQ的面积最大？最大面积是多少？

(3)　　　 若用一条直线将梯形OABC分为面积相等的两部分，试说明你的分法。

24、如图，平面直角坐标系中，四边形OABC为矩形，点A和B的坐标分别为(3，0)和(3，4)。动点M和N分别从O和B同时出发，以每秒1个单位的速度运动。其中点M沿OA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥BC，交AC于点P，连接MP。已知动点运动了。

①P点的坐标为(　　　 ，　　　　 )。用含x的代数式表示

②试求△MPA面积的最大值，并求此时x的值。

　 ③当x为何值时，△MPA是一个等腰三角形？你发现了几种情况？写出你的研究成果。

23、为了测量校园内一棵不可攀的树的高度，学校数学应用实践小组做了如下的探索：

实践一：根据《自然科学》中的反射定律，利用一面镜子和一根皮尺，设计如右示意图的测量方案：把镜子放在离树(AB)8.7米的点E处，然后沿着直线BE后退到点D，这是恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.7米，观察者目高CD=1.6米，请你计算树(AB)的高度．(精确到0.1米)

实践二：提供选用的测量工具有：①皮尺一根；②教学用三角板一副；③长为2.5米的标杆一根；④高度为1.5米的测角仪(能测量仰角、俯角的仪器)一架。请根据你所设计的测量方案，回答下列问题：

(1)在你设计的方案中，选用的测量工具是(用工　

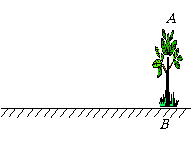具的序号填写)　　　　　　　　　　　　

(2)在右图中画出你的测量方案示意图；

(3)你需要测得示意图中的哪些数据，并分别用a、b、c、α等表示测得的数据： 　　　　　　　　　　　　　　　　　　　　　　

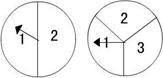
21、小明和小刚用如图的两个转盘做游戏，游戏规则如下：分别旋转两个转盘，当两个转盘所转到的数字之积为奇数时，小明得2分；当所转到的数字之积为偶数时，小刚得1分。这个游戏对双方公平吗？若公平，说明理由，若不公平，如何修改规则才能使游戏对双方公平？

20、尺规作图，写出作法，并保留作图痕迹。

已知线段AB。求作⊙O，使它经过A、B两点；