
7. 为筹备班级的初中毕业联欢会,班长对全班学生爱吃哪几种水果作了民意调查.那么最终买什么水果,下面的调查数据中最值得关注的是 ( )
A.中位数 B.平均数 C.众数 D.加权平均数
6.在匀速运动中,路程s(千米)一定时,速度V(千米/时)关于时间t(小时)的函数关系的大致图象是( )
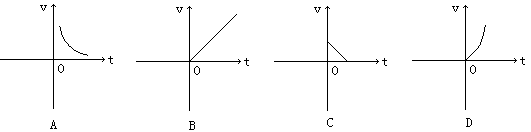
5.在数-4,-2,-1,0,1,2,4中,任意取一个数,使分式 没有意义的概率是 ( )
没有意义的概率是 ( )
A.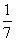 B.
B.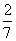 C.
C.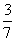 D.
D.
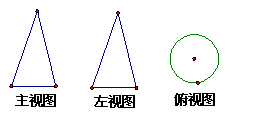
4.某物体的三视图是如图所示的三个图形,
那么该物体的形状是( )
A长方体 ; B圆锥体 ; C 立方体 ; D圆柱体.
3. 把不等式组
把不等式组 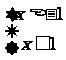 的解集表示在数轴上,正确的是
( )
的解集表示在数轴上,正确的是
( )



|
|
|
|
2. 在0,-1,1,-2这四个数中,最小的数是( )
A.-1 B.0 C.1 D.-2。
有一项是符合题目要求的).
1.-6的绝对值是( )。
A. -6 B. 6 C. - D.
D. 
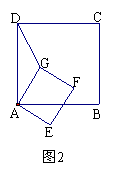
25、图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).
(1)操作:固定△ABC,将△C′D′E′绕点C顺时针旋转30°得到△CDE,连结AD、BE,CE的延长线交AB于F(图2);
探究:在图2中,线段BE与AD之间有怎样的大小关系?试证明你的结论.(4分)
(2)操作:将图2中的△CDE,在线段CF上沿着CF方向以每秒1个单位的速度平移,平移后的△CDE设为△PQR(图3);
探究:设△PQR移动的时间为x秒,△PQR与△ABC重叠部分的面积为y,求y与x之间的函数解析式,并写出函数自变量x的取值范围.(5分)
(3)操作:图1中△C′D′E′固定,将△ABC移动,使顶点C落在C′E′的中点,边BC交D′E′于点M,边AC交D′C′于点N,设∠AC C′=α(30°<α<90°=(图4);
 探究:在图4中,线段C′N·E′M的值是否随α的变化而变化?如果没有变化,请你求出C′N·E′M的值,如果有变化,请你说明理由.(4分)
探究:在图4中,线段C′N·E′M的值是否随α的变化而变化?如果没有变化,请你求出C′N·E′M的值,如果有变化,请你说明理由.(4分)
结束语:再仔细检查一下,也许你会做得更好,祝你成功!
24、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请证明,若不正确请举反例说明;

 (2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
23、右图是佛山某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如下图).
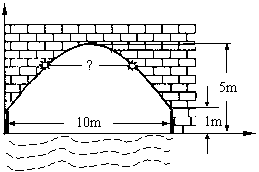 (1)求抛物线的解析式.
(1)求抛物线的解析式.
(2)求两盏景观灯之间的水平距离.
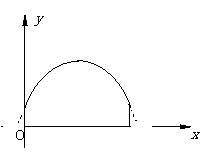
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com