
4.半径为4和8的两圆相内切,则圆心距为( )
A.4 B.8 C.12 D.16
3.下列说法正确的是( )
A 近似数1.450有三个有效数字 B 多项式a2b-3b+1是二次三项式
C 0.0109用科学记数法表示为1.09×10-4 D 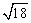 与
与 是同类二次根式
是同类二次根式
2.当我们从上面观察图1所示的两个物体时,看到的将是( )

1.下列7个数  ,3.1415926,(π-2)0,-3,
,3.1415926,(π-2)0,-3, ,-
,- ,0 中,有理数有( )个
,0 中,有理数有( )个
A、4 B、2 C、3 D、5
 21)如图,在□ABCD中,点E、F在对角线上,且AE=CF,请你以点F为一个端点,与图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的哪一条线段相等(只需证明一组线段相等即可)
21)如图,在□ABCD中,点E、F在对角线上,且AE=CF,请你以点F为一个端点,与图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的哪一条线段相等(只需证明一组线段相等即可)
(1)连结: 。
(2)猜想 。
(3)证明;
22)如图,一张边长为16㎝的正方形硬纸板,把它的四个角都剪去一个边长为x㎝的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为V㎝3,
请回答下列问题:
(1)若用含有X的代数式表示V,则V= (3分)
(2)完成下表:(4分)
|
x(㎝) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
V(㎝3) |
196 |
288 |
|
|
180 |
96 |
28 |
 (3) 观察上表,容积V的值是否随x值得增大而增大?当x取什么值时,容积V的值最大?(3分)
(3) 观察上表,容积V的值是否随x值得增大而增大?当x取什么值时,容积V的值最大?(3分)
23)某校要从小王和小李两名同学中挑选一人参加全国数学竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:

根据上表解答下列问题:
(1)完成下表:(5分)
|
姓名 |
极差(分) |
平均成绩(分) |
中位数(分) |
众数(分) |
方差 |
|
小王 |
40 |
80 |
75 |
75 |
190 |
|
小李 |
|
|
|
|
|
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?(3分)
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由(2分)
24)用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.
(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图13-1),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论;(5分)
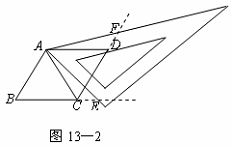
 (2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图13-2),你在(1)中得到的结论还成立吗?简要说明理由.(5分)
(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图13-2),你在(1)中得到的结论还成立吗?简要说明理由.(5分)
25)某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量 (万件)与销售单位
(万件)与销售单位 (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系.
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)试写出该公司销售该种产品的年获利 (万元)关于销售单价
(万元)关于销售单价 (元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价
(元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价 为何值时,年获利最大?并求这个最大值;
为何值时,年获利最大?并求这个最大值;
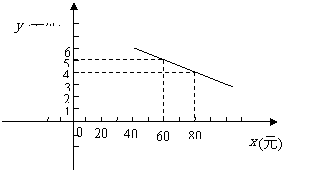 (3)若公司希望该种产品一年的销售获利不低于40万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
(3)若公司希望该种产品一年的销售获利不低于40万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
16)先化简,再求值:(1 )÷
)÷ 其中
其中
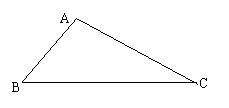 17)有一块三角形的地,现要分给两户人家(既要二等分三角形面积)。请你在图中作出分法,并写出做图的步骤。
17)有一块三角形的地,现要分给两户人家(既要二等分三角形面积)。请你在图中作出分法,并写出做图的步骤。
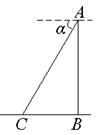
18) 如图,点C与建筑物AB底部B的水平距离BC=15米,从点A测得点C的俯角α=60°,求建筑物AB的高.(结果保留根号)
19)一个口袋中放有20个球,其中红球6个,白球和黑球各若干个,每个球除了颜色以外没有任何区别。小王通过大量反复的实验(每次取一个球,放回搅匀后再取第二个)发现,取出黑球的频率稳定在 左右,请你估计袋中黑球的个数;
左右,请你估计袋中黑球的个数;
20)如图是某汽车行驶的路程S(km)与时间t(min) 的函数关系图.观察图中所提供的信息,解答下列问题:
 (1)汽车在前9分钟内的平均速度是多少?
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式.
 11)如图3,已知AB∥CD,CE、AE分别平分∠ACD、∠CAB,
11)如图3,已知AB∥CD,CE、AE分别平分∠ACD、∠CAB,
则∠1+∠2= 。
12)函数 的自变量x的取值范围是 。
的自变量x的取值范围是 。
13)不等式组  的解集为
。
的解集为
。
14) 已知圆锥的底面半径为2cm,母线长为3cm,则该圆锥的侧面展开图的面积为______________cm2。
 15)如图(1),是一个三角形ABC,它的三边长分别为
15)如图(1),是一个三角形ABC,它的三边长分别为 ,分别连接这个三角形三边的中点,得△
,分别连接这个三角形三边的中点,得△ ,如图(2);再分别连接中间这个三角形三边的中点,得△
,如图(2);再分别连接中间这个三角形三边的中点,得△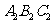 ,如图(3);按此方法继续下去,请你根据每个图中三角形边长的规律,写出△
,如图(3);按此方法继续下去,请你根据每个图中三角形边长的规律,写出△ 的周长为
。
的周长为
。
1)一个数的相反数是3,则这个数是( )
A. B.
B.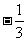 C.
C.  D.
D. 
2)长城总长约为6 700 000米,用科学记数法表示是( ) (保留两个有效数字)
A.6.7×105米 B.6.7×106 米 C.6.7×107 米 D.6.7×108米
3)我们从不同的方向观察同一物体时,可以看到不同的平面图形.如图1,从图的左面 看这个几何体的左视图是 (
)
看这个几何体的左视图是 (
)

A B C D
4)下列各式运算正确的是( )
A.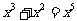 B.
B. C.
C. D.
D.
5)已知两圆的半径分别为2和4,圆心距为6,则两圆的位置关系是( )
A.外离 B.外切 C.相交 D.内切
 6)函数
6)函数 的图象过点
的图象过点 ,则此函数的图象在平面直角坐标系中的第( )象限
,则此函数的图象在平面直角坐标系中的第( )象限
A.一、三 B.三、四 C.一、二 D. 二、四
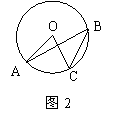
7)如图2,A、C、B是⊙O上三点,若∠AOC=40°,则∠ABC的度数是( )
A.10° B.20° C.40° D.80°
8)下列四幅图形中,表示两颗小树在同一时刻阳光下的影子图形可能是( )
 9)中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏. 游戏规则如下:在20个商标牌中,有5个商标牌的背面注明了一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸就不得奖. 参与这个游戏的观众有三次翻牌的机会. 某观众前两次翻牌均获得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是
9)中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏. 游戏规则如下:在20个商标牌中,有5个商标牌的背面注明了一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸就不得奖. 参与这个游戏的观众有三次翻牌的机会. 某观众前两次翻牌均获得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是
A. B.
B. C.
C.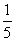 D.
D.
10) 下列调查方式,你认为正确的是 ( )
A. 了解一批炮弹的杀伤半径,采用普查方式
B. 了解佛山市每天的流动人口数,采用抽查方式
C. 要保证“神舟6号”载人飞船成功发射,对重要零部件采用抽查方式检查
D. 了解佛山市居民日平均用水量,采用普查方式
25、已知⊙ 的半径为1,以
的半径为1,以 为原点,建立如图所示的直角坐标系.有一个正方形
为原点,建立如图所示的直角坐标系.有一个正方形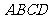 ,顶点
,顶点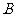 的坐标为(
的坐标为( ,0),顶点
,0),顶点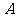 在
在 轴上方,顶点
轴上方,顶点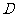 在⊙
在⊙ 上运动.
上运动.
(1)当点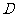 运动到与点
运动到与点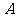 、
、 在一条直线上时,
在一条直线上时, 与⊙
与⊙ 相切吗?如果相切,请说明理由,并求出
相切吗?如果相切,请说明理由,并求出 所在直线对应的函数表达式;如果不相切,也请说明理由;
所在直线对应的函数表达式;如果不相切,也请说明理由;
(2)设点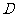 的横坐标为
的横坐标为 ,正方形
,正方形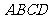 的面积为
的面积为 ,求出
,求出 与
与 的函数关系式,并求出
的函数关系式,并求出 的最大值和最小值.
的最大值和最小值.

24、有一个未知圆心的圆形工件.现只允许用一块直角三角板(注:不允许用三角板上的刻度)画出该工件表面上的一根直径并定出圆心.要求在图上保留画图痕迹,写出画法.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com