
5.已知向量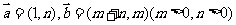 教育博客,若
教育博客,若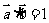 ,则
,则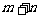 的最小值为( )
的最小值为( )
A.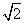 B.
B.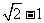 C.
C.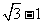 教育博客 D.
教育博客 D.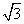
4.方程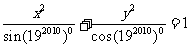 所表示的曲线是( )
所表示的曲线是( )
A.双曲线 B.焦点在x轴上的椭圆教育博客
C.焦点在y轴上的椭圆 D.以上答案都不对教育博客
3.某校在高二年级开设选修课,其中数学选修课开三个班,选课结束后,有四位同学要求改修数学,但每班至多可再接收2位同学,那么不同的分配方案有( )
A.72种 B.54种 C.36种 D.18种
2.在 ABC中已知2
ABC中已知2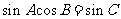 ,那么
,那么 ABC一定是( )
ABC一定是( )
A.直角三角形 B.等腰三角形 C.正三角形 D.等腰直角三角形
1.设集合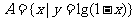 ,集合
,集合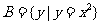 ,则A
,则A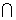 B=( )
B=( )
A.( )
B.
)
B. C.[
C.[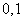 ] D.
] D.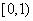
2.比较大小.

课堂小结:对数函数的图像与性质
作业:习题3-5A组3,4,5,6
1.求下列函数的定义域:
(1)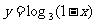
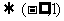
(2)
(3)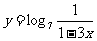

(4)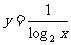

2.练习:画出下列函数的图像
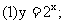
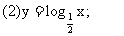
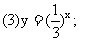
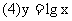
下面对对数函数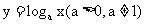 分别就其底数
分别就其底数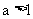 和
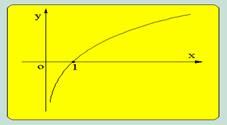
和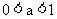 这两种情况的图像和性质为:
这两种情况的图像和性质为:
|
函 数 |
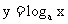 (a>1) (a>1) |
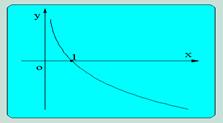
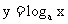 (0<a<1) (0<a<1) |
|
图 像 |
 |
 |
|
定义域 |
(0,+∞) |
(0,+∞) |
|
值 域 |
R |
R |
|
单调性 |
增函数 |
减函数 |
|
过定点 |
(1,0) |
(1,0) |
|
取值范围 |
0<x<1时,y<0 x>1时,y>0 |
0<x<1时,y>0 x>1时,y<0 |
例4.求下列函数的定义域:
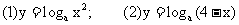
解:(1)因为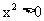 ,即
,即 ,所以函数
,所以函数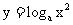 的定义域为
的定义域为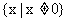 ;
;
(2)因为 ,即
,即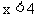 ,所以函数
,所以函数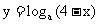 的定义域为
的定义域为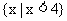
练习1:求下列函数的定义域
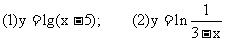
解:
(1)因为 ,即
,即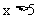 ,所以函数
,所以函数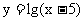 的定义域为
的定义域为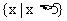
(2)因为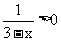 ,即
,即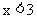 ,所以
,所以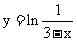 的定义域为{x∣x<3}
的定义域为{x∣x<3}
例5.比较下列各题中两个数的大小:
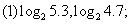
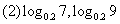
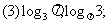
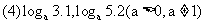
分析:本题中对于同底数的对数利用对数函数的单调性来解决,对于不同底的对数则注意(4)的分类讨论。
解:
(1)因为2>1,函数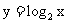 是增函数,5.3>4.7,所以
是增函数,5.3>4.7,所以
(2)因为0.2<1,函数 是减函数,7<9,所以
是减函数,7<9,所以 ;
;
(3)因为函数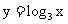 是增函数,
是增函数,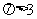 ,所以
,所以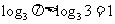 ,同理
,同理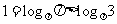 ,所以
,所以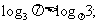
(4)对数函数的单调性取决于其底数是大于1还是小于1,而已知条件中并没有明确指出底数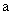 与1哪个大,因此需要对底数进行同理.
与1哪个大,因此需要对底数进行同理.
当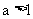 时,函数
时,函数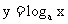 在
在 上是增函数,此时,
上是增函数,此时, 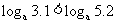 ,
,
当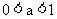 时,函数
时,函数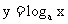 在
在 上是减函数,此时,
上是减函数,此时, 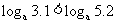
练习2:比较下列各组数中两个值的大小:
(1)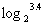 ,
,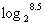 (<=
(<=
(2)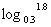 ,
,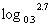 (>)
(>)
(3)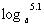 ,
,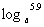 (a>0,且a≠1)
(a>1时,<,0<a<1时,>=
(a>0,且a≠1)
(a>1时,<,0<a<1时,>=
课堂补充练习:
3、情感.态度与价值观
使学生通过学习对数函数,了解指数函数与对数函数图像和性质之间的关系.在学习的过程中体会类比、转化、数形结合的方法研究问题.直观明了,增强学习对数函数的积极性和自信心.
[教学重点]: 对数函数的图像和性质以及与指数函数图像与性质之间的关系.
[教学难点]:对数函数图像与性质与指数函数的图像与性质之间的关系.
[课时安排]: 2课时
[学法指导]:学生思考、探究.
[讲授过程]

[新课导入]
[互动过程1]
复习:1.对数函数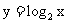 的图像与性质,以及与指数函数
的图像与性质,以及与指数函数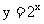 的图像与性质之间的关系
的图像与性质之间的关系
2、 过程与方法 
(1)让学生掌握指数函数的图像与对数函数的图像之间的关系,会利用它们的对称关系,
熟练地进行画图.
(2)学会类比研究问题,利用数性结合的思想研究函数的性质.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com