
3.若集合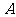 是
是 个元素的集合,则集合
个元素的集合,则集合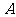 有
有 个子集(其中
个子集(其中 个真子集,
个真子集, 个非空真子集).
个非空真子集).
典例剖析
[题型1] 集合元素的基本特征
[例1]已知集合 ,试求集合
,试求集合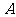 的所有子集.
的所有子集.
[解析]由题意可知 是
是 的正约数,所以
的正约数,所以
 可以是
可以是 ;相应的
;相应的 为
为
 ,即
,即  .
.
∴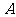 的所有子集为
的所有子集为 .
.
[点评] 本题主要考查集合的基础知识,集合中的元素具有确定性、互异性与无序性三大特性,尤其是互异性在解题中应予以足够重视.
[变式与拓展]
2.集合有三种表示方法
列举法:把集合中的元素一一列举出来,写在大括号内;
描述法:把集合中的元素的公共属性描述出来,写在大括号 内.
内.
具体方法:在花括号内先写上表示这个集合元素的一般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征.
注意:列举法与描述法各有优点,应该根据具体问题确定采用哪种表示法,要注意,一般集合中元素较多或有无限个元素时,不宜采用列举法.
1.集合中的元素必须具有:确定性、互异性与无序性。确定性:设A是一个给定的集合,x是某一个具体对象,则或者是A的元素,或者不是A的元素,两种情况必有一种且只有一种成立;互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素;无序性:集合中不同的元素之间没有地位差异,集合中元素的排列不是固定的;
2.集合间的关系:
(1)集合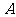 的任何一个元素都是集合
的任何一个元素都是集合 的元素,则称
的元素,则称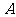 是
是 的子集(或B包含
的子集(或B包含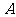 ),记作
),记作 .
.
(2)集合相等:构成两个集合的元素完全一样,若 且
且 ,则称
,则称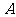 等于
等于 ,记作
,记作 .
.
(3)若 且
且 ,则称
,则称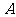 是
是 的真子集,或者若
的真子集,或者若 ,但存在元素
,但存在元素 且
且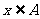 ,则称
,则称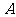 是
是 的真子集,记作
的真子集,记作 .
.
(4)不含任何元素的集合称为空集,记作 .规定:空集是任何集合的子集.
.规定:空集是任何集合的子集.
(5)简单性质:1) ;2)
;2) ;3)若
;3)若 ,
, ,则
,则 .
.
教材透析
1.集合的含义与表示
(1)一般地,把一些指定的对象组成的总体叫做集合,集合中的对象称元素,若a是集合A的元素,记作 ;若b不是集合
;若b不是集合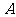 的元素,记作
的元素,记作 ;
;
(2)集合中的元素必须满足:确定性、互异性与无序性三大特性;
(3)常用的集合表示法:列举法、描述法或图示法( 图);
图);
(4)常用数集及其记法:
非负整数集(或自然数集),记作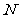 ;正整数集,记作
;正整数集,记作 或
或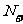 ;整数集,记作
;整数集,记作 ;
;
有理数集,记作 ;实数集,记作
;实数集,记作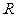 .
.
3.集合的基本运算
(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;
(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;
(3)能使用 图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.
图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.
[知识网络]

第一节 集合的概念与相互关系
自主学习
2.集合间的基本关系
(1)理解集合之间包含与相等的含义,能识别给定集合的子集;
(2)在具体情境中,了解全集与空集的含义;
1.集合的含义与表示
(1)通过实例,了解集合的含义,体会元素与集合的“属于”关系;
(2)能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用;
20.这是挂在岳麓山正门的对联,下联已被拆散且打乱排列顺序,如将拆乱的下联重新组合,则正确的顺序应为(填字母即可):___________________(3分) 上联:学正朱张,一代文风光大麓 下联:A、浩气 B、黄蔡 C、勋高 D、震名山 E、千秋
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com