
2、掌握二项式定理,会用展开式通项求有关展开式的问题。
1、排列数、组合数的计算、化简、证明等;会解排列、组合应用题,掌握常见应用题的处理思路。
燕子是候鸟,它们每年春天都要到北方来,小燕子就在这个时候出生的。当燕子孵化出来,慢慢长出一点翅膀的时候,燕子妈妈就要教它如何人飞翔了。
今天可和往常不一样,往常总是燕子妈妈将小虫叼到燕子窝里来喂,可是今天已经到晚上了,小燕子还没有吃早餐。燕子妈妈嘴里叼着食,就在不远处飞翔,小燕子饿坏了。妈妈怎么还不给宝宝喂食呀?
“来吧,孩子,试着飞过来。”
“妈妈,我不敢,我不会飞呀!离地太高了,万一摔下来怎么办呀?”
燕子妈妈什么也没有说,只是在空中盘旋着。过了一会儿,有个胆子大一点的小燕子先探探脑袋。
“孩子,来吧!你能行,我也是这样学会飞的。试着拍打翅膀,对,对了,就这样,很好,你成功了!妈妈为你高兴。”一只燕子飞出巢,它成功了。
接着第二个,第三个小家伙也成功了。
最后一个小家伙,胆子特小,不敢飞。
“妈妈,我不敢飞。“
“来吧,飞是迟早的事情毛窝们还要飞越高山、大海,不会飞,怎么行呢!你的哥哥,姐姐已经会飞了。学习它们,勇敢一点。“
实在太饿了。小燕子只好一跃而起,朝妈妈的方向飞去。
“哎哟!我掉到地上了。”小燕子趴在地上痛苦地说。
“没有摔伤,试着飞起来,再来一下,我这里有吃的。”燕子妈妈飞得底一些,鼓励小燕子。
燕子看着慈祥的妈妈,看着勇敢的哥哥、姐姐,拍打翅膀,试着飞了起来。
“真好,你也成功了!”哥哥和姐姐高兴地祝贺它。


附录:2
“草原探险夏令营:中日两国孩子的不同表现”
1992年8月,中日两国儿童在内蒙古举办一个草原探险夏令营。这些孩子的年龄都在11岁到16岁之间,但中日两国的孩子在夏令营的表现截然不同:日本的孩子黑木堆界肚子疼,脸色苍白,汗珠直流,但仍坚持前行;一位中国的女孩子刚走几步就走不动了,见了医生眼泪汪汪,她被送回大本营。途中,日本的孩子行囊满满的。中国的孩子的行囊只是装样子,都是空空的。到了宿营地,日本的孩子将香肠、黄瓜、柿子椒等混在一起炒,又熬了米粥;抄着手什么也不干的全是中国孩子。老师批评他们不劳而获,他们木然无语。日本
的孩子将用过的杂物,都用塑料袋装起来,而中国的孩子,一边走一边丢。日本的孩子见到百灵鸟蛋,马上用木棍围起来,而中国的孩子却不能这样做。

附录:3

我的自立计划-____ 第_天,共_天 今天是_年_月_日 星期_  本月的目标:    今天值得记录的:      我的感悟:     |



第二课时:
告别依赖
走向自立
教学环节:
小品导入:
学生表演课前准备好的小品:小雅的一天
学生看完后分析并思考问题:从身边依赖的事例,谈依赖的坏处。教师介绍依赖的事例、危害(见教材招聘会上的一幕和教参)后提问
:培养独立是不是都得象小雅再独立生活?学生交流后,教师归纳依赖的危害并对依赖产生的问题进行讲解,说明自己不是拒绝帮助,依靠不是依赖。
活动一:今昔对比
教师直接指出课本第39页“中小学生对比”的事例:分析交错上给出的三种说法,还可以补充其他的说法。
小结:
我们在社会中生活,需要相互帮助,相互依靠。自立不是拒绝帮助,依靠不是依赖。幼小的时候我们对父母、长辈有所“依赖”是自然的,也是必要的。随着年龄的增长,自立能力的增强,我们日益希望自己能象成年那样管理自己的生活。
活动二:看图
观看课本第41页“女学生由睡懒觉到自己起床上学”的四幅图片,来分析女学生睡懒觉的原因,以及改正的原因;反思自己身上类似的现象。
资料;“美国里根”小时候的故事(见附录)
小结
自立的一个重要表现是独立地生活。要独立生活,就要做到自己的事情自己负责。只要明确自己的主任,勇于承当自己的责任,才能成为真正自立的人。当然。自己的事情自己的负责的前提是要自主。没有主见,人云亦云的人是不能承当责任的,更无法自立。所以自主是自立的前提。
活动三:行动
过渡:当人们有了独立自主的愿望,几自主的意识后,又该怎样培养自己的自主能力呢?
从学生所搜索的世界各国青少年自立状况总结自立的方法:立足当前生活、学习中的问题,从小事做起;大胆的投身社会实践并反复锻炼。
引导学生讲述自己在自立方面的事例,增加感性认识。
本节小结
引导学生总结:学习本节课的体会和收获。(只要能说出:依赖有危害;自主是自立的前提;要自立就要从生活中的小事做起,大胆实践,反复锻炼就可以。)
作业布置
《学习与评价》相关练习
附录:
1920年,有个11岁的美国男孩子踢足球不小心打碎了邻居家的玻璃,人家索赔12.5美元`,当时12.5美元可以买125只生蛋的母鸡。闯出大祸的男孩向父亲认错,父亲让他对自己的事情负责,儿子为难的说:“我没钱赔给人家。”父亲说:“这12.5美元我借给你,一年后还给我。”从此,男孩子开始了艰苦的打工生活。经过半年的努力终于挣足了2.5美元,还给了父亲。这个男孩就是成为美国总统的里根。里根在会议这件事的时候说:“通过自己的劳动来承担过失,使他懂得了什么叫做责任。”
21.(本小题满分14分)已知函数 (其中
(其中 为自然对数的底数),
为自然对数的底数),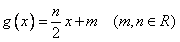 。
。
(Ⅰ)若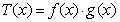 在
在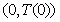 处的切线与直线
处的切线与直线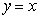 平行,试用
平行,试用 表示
表示 ,并求此时
,并求此时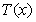 在
在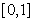 上的最大值;
上的最大值; 
(Ⅱ)若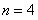 时方程
时方程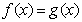 在
在 上恰有两个相异实根,求
上恰有两个相异实根,求 的取值范围;
的取值范围;
(Ⅲ)在 ,
,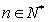 时,求使
时,求使 的图象恒在
的图象恒在 图象上方的最大自然数
图象上方的最大自然数 。
。
20.(本小题满分13分)已知二次函数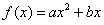 (
( 为常数且
为常数且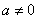 ),满足条件
),满足条件 ,且方程
,且方程 有等根.
有等根.
(Ⅰ)求 的解析式;
的解析式; 
(Ⅱ)设
 的反函数为
的反函数为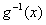 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)是否存在实数 ,使
,使 的定义域和值域分别为
的定义域和值域分别为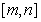 和
和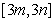 ,如果存在,求出
,如果存在,求出  的值,如果不存在,说明理由.
的值,如果不存在,说明理由.
19.(本小题满分12分)函数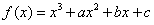 ,曲线
,曲线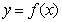 上的点
上的点 处的切线方程为
处的切线方程为
(Ⅰ)若 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,求 上最大值;
上最大值; 
(Ⅲ)若函数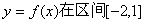 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
18.(本小题满分12分)某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
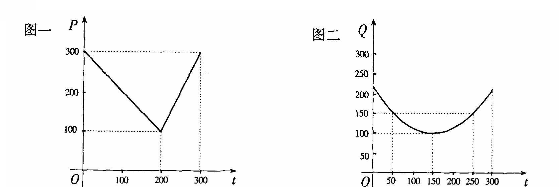
(Ⅰ) 写出图一表示的市场售价与时间的函数关系式P=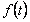 ;写出图二表示的种植成本与时间的函数关系式Q=
;写出图二表示的种植成本与时间的函数关系式Q=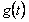 ;
; 
(Ⅱ) 认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/ kg,时间单位:天)
kg,时间单位:天)
17.(本小题满分12分)如图,正四棱锥P-ABCD中,侧面与底面ABCD所成角为60°,点E是PB的中点。
(Ⅰ)求异面直线PD与AE所成角的大小;

(Ⅱ)求二面角P-AC--E的大小;
(Ⅲ)在侧面PAD上是否存在一点F,使EF⊥平面PBC,
若存在,确定点F的位置,并证明;若不存在,说明理由。
16.(本小题满分12分)已知集合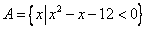 ,集合
,集合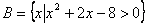 ,集合
,集合 ,
, 
(Ⅰ)求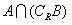 ; (Ⅱ)若
; (Ⅱ)若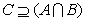 ,试确定实数
,试确定实数 的取值范围.
的取值范围.
15. 一个圆的面积以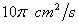 的速率增加,那么当圆的半径
的速率增加,那么当圆的半径 时,其半径
时,其半径 增加的速率
增加的速率 为
为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com