
 读图,回答10-11题。
读图,回答10-11题。
10.图中显示开罗与武汉的气候要素特征相差悬殊,造成这一现象主要是
A.两地地形差异 B.距海远近差异
C.所受大气环流差异 D.纬度位置差异
11.图中阴影对应的时节,控制武汉的天气系统主要是

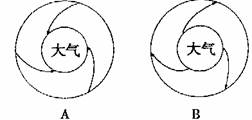
9.下列各图中,正确表示引发泥石流因子的是

下图表示几种自然灾害的持续时间。读图完成7-8题。

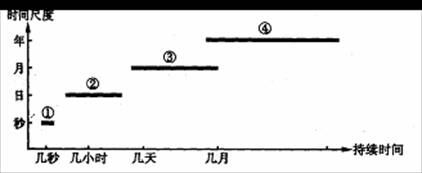
7.①②③④四种灾害分别是
A.火山、地震、干旱、洪涝 B.地震、火山、洪涝、干旱
C.干旱、洪涝、地震、火山 D.火山、地震、洪涝、干旱
8.蝗虫是危害严重的生物灾害。图中所示的自然灾害中,与其发生密切相关的是
A.①② B.②④ C.①②③ D.③④
读生态学家研究气候对植被的影响时绘制的《生态气候图》。根据《a地气候类型示意图》上所作的说明,分析位于我国东部平原地带的b、c两地的气候类型示意图,并回答5-6题。
 t x
t x
5.从充分利用当地农业气候资源、取得农作物生产的最佳社会经济效益角度考虑,b、c两地合理的农业种植制度是
①b地为一年三熟,双季稻加冬作油菜 ②b地为一年二熟,小麦复种花生或棉花 ③c地为一年二熟,冬小麦复种玉米或谷子④c地为一年二熟,春小麦、玉米与大豆隔年轮作
A.②④ B.①③ C.①② D.③④
6.能够减轻c地农业气象灾害的有效措施是
①用人造烟雾来防御霜冻 ②跨流域调水来抵御伏旱 ③修建水库来防洪抗旱 ④超采地下水来缓解春旱
A.①② B.①③ C.③④ D.②④
图中数字代号表示广州、圣地亚哥、乌鲁木齐、吉隆坡4个城市。完成1-4题。
1.图中4个城市附近地形最不易形成滑坡等地质灾害的是
 A.① B.② C.③ D.④
A.① B.② C.③ D.④
2.关于四个城市中滑坡等地质灾害多发区地理特征的叙述,正确的是
①地形崎岖 ②全年降水丰富,年际变化大
③地表基岩广布 ④地表岩石破碎,松散碎屑物多
A.①④ B.②③ C.①② D.②④
3.下列属于预防滑坡工程措施的是
A.修建水库 B.迁移居民
C.砌石护面、设置排水沟 D.建立监测网络
4.图中4个城市中,北半球冬至日正午太阳高度最大的是
A.① B.② C.③ D.④
(三)练习作业
1.设a、b为两条直线,α、β为两个平面,下列四个命题中,正确的命题是( )
A.若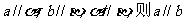 B.若
B.若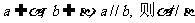
C.若 D.若
D.若
2平面α∥平面β的一个充分条件是( )
A.存在一条直线a, a∥α, a∥β B.存在一条直线a,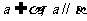
C.存在两条平行直线a、b,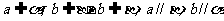
D.存在两条异面直线a、b,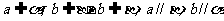
3.ABCD为梯形,P在平面ABCD外,AD⊥面PAB,BC⊥面PAC,底面ABCD为梯形,AD=4,BC=8,AB=6,∠APD=∠CPB,满足上述条件的P的轨迹是( )
A.圆 B.不完整的圆 C.抛物线 D.抛物线的一部分
4.底面是直角梯形的四棱锥P-ABCD中,PA⊥底面ABCD,BC∥AD,∠ABC=900,PA=AB=BC=2,AD=1,则D到平面PBC的距离为 。
5.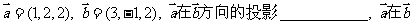 方向上的射影为 。
方向上的射影为 。
6.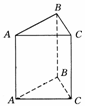 直三棱柱ABC-A1B1C1中,∠ACB=900,∠BAC=300,BC=1,
直三棱柱ABC-A1B1C1中,∠ACB=900,∠BAC=300,BC=1,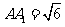 ,M是CC1中点。求证:AB1⊥A1M。
,M是CC1中点。求证:AB1⊥A1M。
7.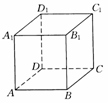 在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且
在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且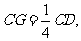 H为C1G的中点。
H为C1G的中点。
(1)求证:EF⊥B1C;(2)求EF与C1G所成的角的余弦值;(3)求FH的长。
(一)小题练习
1、长方体ABCD-A1B1C1D1中,∠DAD1=450,∠CDC1=300,异面直线AD1与DC1所成角的大小是 。
2、对于一个底边在x轴上的三角形,采用斜二测画法作出其直观图,则直观图面积是原三角形面积的 倍。
3、已知线段AB⊥平面α,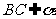 ,CD⊥BD,异面直线AB、CD所成角600,D与A在α的同侧,若AB=BC=CD=2,求AD= 。
,CD⊥BD,异面直线AB、CD所成角600,D与A在α的同侧,若AB=BC=CD=2,求AD= 。
4、ΔABC中,AB=10,AC=6,BC=8,点P是ΔABC所在平面外一点,且P到ΔABC三边距离等于12,则P到面ABC的距离为 。
5、已知ABCD为正方形,P是ABCD所在平面外一点,P在平面ABCD上的射影恰好是正方形的中心O,Q是CD中点,求下列各项中的x、y值。
(1)
(2)
 (二)例题
(二)例题
例1,四面体A-BCD中,以下成立的有几个?
①若AB=AC,BD=CD =>BC⊥AD
②若AB=BD,AC=CD=>BC⊥AD
③若AB⊥AC,BD⊥CD=>BC⊥AD
④若AB⊥CD,AC⊥BD=>BC⊥AD
⑤若D在AB上的射影为ΔABC的垂心=>B在ACD上的射影必为
ΔACD垂心。
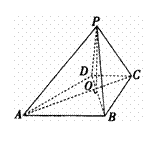
例2,如右图,等腰梯形ABCD中,AB∥CD,AC⊥BD,
AC∩BD=O,平面ABCD外一点P满足PO⊥平面ABCD,又BO=2,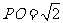 ,PB⊥PD。
,PB⊥PD。
(1)求异面直线PD与BC所成角的余弦值;
(2)求平面PAB的法向量与平面CAB的法向量所成角的大小;
(3)设点M在棱PC上,且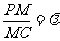 ,问λ为何值时,
,问λ为何值时,
PC⊥平面BMD?
例3,已知四棱锥S-ABCD的底面边长为4的正方形,S在底面上的射影O落在正方形ABCD内,且O到AB、AD的距离分别为2、1。
(1)求证: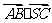 是定值;(2)已知P是SC的中点,且SO=3,问在棱长A上是否存在一点Q,使异面直线OP与BQ所成角900。
是定值;(2)已知P是SC的中点,且SO=3,问在棱长A上是否存在一点Q,使异面直线OP与BQ所成角900。
例4,ΔABC中,AC=13,AB=5,BC=12且PA=PB=PC=8,求P到面ABC距离。
ΔABC中,AB=5,BC=8,∠ABC=1200,PA=PB=PC=12,求P到面ABC距离。
ΔABC中,AB=10,AC=6,BC=8,P是ΔABC所在平面外一点,且P到三边距离等于12,则P到面ABC距离。
1、共线向量
(1)对于空间任意两个向量
(2)A、B、C共线的充要条件是:
①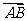 = ;
= ;
② ,且 ;
,且 ;
③若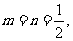 则C是
则C是
2、共面向面
(1)对于空间不共线向量
(2)P与不共线三点A、B、C共面充要条件是:
①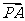 =
=
② ,且
,且
③若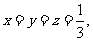 则P为
则P为
3、数量积
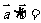
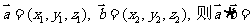
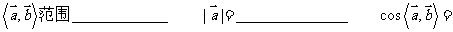
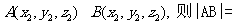
4、投影
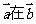 方向的投影为
方向的投影为
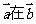 方向的射影为
方向的射影为
5、( )=> 线⊥面
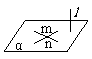
4、 ( )=>
线⊥线
( )=>
线⊥线

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com