21．已知函数f (x) = 2x²，g (x) = a lnx (a＞0)，

　　 (1)若直线l交f (x)的图象C于A、B两点，与l平行的另一直线l′切图象C于点M，求证：A、M、B三点的横坐标成等差数列；

　　 (2)若不等式f (x)≥g (x)恒成立，求a的取值范围；

　　 (3)求证：(其中e为无理数，约为2.71828)．

20．若椭圆E₁：和椭圆E₂：，则称这两个椭圆相似，m称为其相似比．

(1)求经过点，且与椭圆相似的椭圆方程；

(2)设过原点的一条射线l分别与(1)中的两个椭圆交于A、B两点(其中点A在线段OB上)，求|OA|·|OB|的最大值和最小值．

19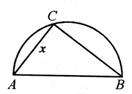．两县城A和B相距距20km，现计划在两县城外以AB为直径的半圆弧上选择一点C建造垃圾处理厂，其对城市的影响度与所选地点到城市的距离有关，对城A和城B的总影响度为对城A与城B的影响度之和，建在C处的垃圾处理厂对城A和城B的总影响度为y，统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为k．当垃圾处理厂建在弧的中点时，对城A和城B的总影响度为0.065．

　　 (1)记C点到城A的距离为x km，将y表示成x的函数；

　　 (2)判断弧上是否存在一点，使建在此处的垃圾处理厂对城A和城B的总影响度最小？若存在，求出该点到城A的距离；若不存在，说明理由．

18．“星光大道”是备受观众喜爱的央视节目，现3位周冠军A、B、C和甲、乙2位挑战者参加12月的月冠军比赛，比赛规则是：第一轮甲、乙2位挑战者从3位周冠军中各选1位进行比赛，胜者进入第二轮比赛，未被选中的周冠军直接进入第二轮比赛；第二轮比赛从3位选手中淘汰1位选手，胜者进入第三轮比赛；第三轮比赛的胜者为月冠军．若每轮比赛中每位选手被淘汰的可能性相等．

　　 (1)求周冠军A、B和挑战者甲、乙进入第一轮比赛且至少有1位挑战者进入第二轮比赛的概率；

　　 (2)求月冠军是挑战者的概率；

　　 (3)设进入第三轮比赛的挑战者的人数为，求的数学期望．

17．一个简单多面体的直观图和三视图如图所示，它的正视图和侧视图都是腰长为1的等腰三角形，俯视图为正方形．

　　 (1)求证：PC⊥BD．

　　 (2)求点C到平面PAB的距离．

16．已知函数f (x) = A sin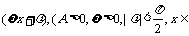R)的图象的一部分如下图所示．

(1)求函数f (x)的解析式；

(2)当x，求函数y = f (x) + f (x + 2)的最大值与最小值及相应的x的值．

15．定义：在数列{a_n}中，n∈N₊，p为常数)，则称{a_n}为“等方差数列”．下列是对“等方差数列”的判断：

　　 ①若{a_n}是等方差数列，则{}是等差数列；

②{(–1)ⁿ}是等方差数列；

③若{a_n}是等方差数列，则{a_kn} (k∈N₊，k为常数)也是等方差数列；

④若{a_n}既是等方差数列，又是等差数列，则该数列为常数列．

其中正确命题序号为　　　　　　 ．

14．如图，在△ABC中，点O是BC的中点，过点O的直线交直线AB、AC于不同的两点M、N，若，则m + n的值为　　　　　　 ．

13．已知：的最大值是　　　 ．

12．曲线的两个交点的距离是　　　　　 ．