
4. 如图甲中
如图甲中 为导体做成的框架,其平面与水平面成
为导体做成的框架,其平面与水平面成 角,质量为
角,质量为 的导体棒
的导体棒 与
与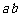 、
、 垂直且接触良好,回路的电阻为
垂直且接触良好,回路的电阻为 ,整个装置放于垂直框架平面的变化的磁场中,磁感应强度
,整个装置放于垂直框架平面的变化的磁场中,磁感应强度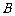 随时间变化规律如图乙所示,棒
随时间变化规律如图乙所示,棒 始终静止,在时间
始终静止,在时间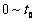 内,棒
内,棒 受到的静摩擦力的大小变化是 ( )
受到的静摩擦力的大小变化是 ( )
A.一直减小 B.一直增大
C.先减小后增大 D.先增大后减小
3.如图虚线上方空间有匀强磁场,扇形导线框绕垂直于框面的轴O以角速度ω匀速转动,线框中感应电流方向以逆时针为正,则能正确表明线框转动一周感应电流变化情况的是 ( )

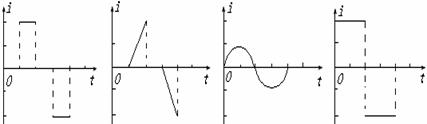
A B C D
2.如图所示,一个闭合线圈套上条形磁铁靠近N极这一端,当在线圈中通以图示方向的电流I时,则 ( )
 A.线圈圆面将有被拉大的倾向
A.线圈圆面将有被拉大的倾向
B.线圈圆面将有被压小的倾向
C.线圈将向上平移
D.线圈将向S极一端平移
1.如图所示水平面上固定一个由均匀金属杆制成的“ ”导轨
”导轨 ,
,  =370,匀强磁场的方向与导轨所在平面垂直,磁感应强度B=0.4
=370,匀强磁场的方向与导轨所在平面垂直,磁感应强度B=0.4 ,另一根保持与导轨
,另一根保持与导轨 接触良好,并保持与
接触良好,并保持与 杆垂直。用水平拉力
杆垂直。用水平拉力 向右拉动
向右拉动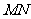 ,使其从
,使其从 点起以
点起以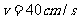 的速度向右匀速运动。金属杆和导轨的电阻都是
的速度向右匀速运动。金属杆和导轨的电阻都是
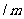 ,其余电阻忽略不计。求回路中的电流
,其余电阻忽略不计。求回路中的电流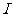 和拉力
和拉力 随时间
随时间 而变化的关系式,并在下面的坐标系中分别做出
而变化的关系式,并在下面的坐标系中分别做出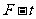 图像和
图像和 图像,标出必要的坐标值。
图像,标出必要的坐标值。

4、电磁感应的过程实质上是不同形式能量转化的过程,电磁感应过程中产生的感应电流在磁场中必定受到安培力的作用,而要维持安培力存在,必须有其它力克服安培力做功,即其它形式的能转化为电能。克服安培力做多少功,就有多少其它形式的能转化为电能。当感应电流通过用电器,电能又转化为内能。由此可见该过程中的能量转化特点为:机械能其它能→电能→内能(焦耳热)。因此,在处理有关电磁感应的内能问题时,可以通过能量守恒定律进行。求解的基本思路是,首先进行正确的受力分析,判断哪些力做功,并确定是正功还是负功,进而明确有哪些形式的能量参与转化,哪增哪减,最后根据能量守恒定律列出方程求解.
[思想方法]
 [例1]如图所示,当滑动变阻器滑动触头向左移动时,右边导轨上导体棒MN向右移动,则a、b两点和c、d两点电势关系是 ( )
[例1]如图所示,当滑动变阻器滑动触头向左移动时,右边导轨上导体棒MN向右移动,则a、b两点和c、d两点电势关系是 ( )
A.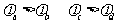 B.
B.
C.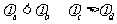 D.
D.
[解析]滑动变阻器滑动触头向左移动时,变阻器连入电路的电阻增加,使得变压器初级线圈电流减小,通过铁芯的磁通量减小,则在次级线圈中产生感应电流. 由于导体棒MN向右移动,则根据左手定则容易判断导体棒中电流向下,则有 ,进一步由安培定则可知此时右边线圈中磁场方向向上;根据楞次定律可以判断左边线圈中磁场方向应该是向下的,同样由安培定则可知左边线圈中电流是从b点进入的,即有
,进一步由安培定则可知此时右边线圈中磁场方向向上;根据楞次定律可以判断左边线圈中磁场方向应该是向下的,同样由安培定则可知左边线圈中电流是从b点进入的,即有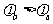 ,因此本题正确答案为C.
,因此本题正确答案为C.
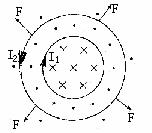
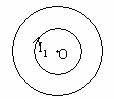 [例2]如图所示为两个同心闭合线圈的俯视图,若内线圈通有图示方向的电流I1,则当I1增大时,外线圈中的感应电流I2的方向及I2受到的安培力F方向分别是:( )
[例2]如图所示为两个同心闭合线圈的俯视图,若内线圈通有图示方向的电流I1,则当I1增大时,外线圈中的感应电流I2的方向及I2受到的安培力F方向分别是:( )
A. I2顺时针方向,F沿半径指向圆心
B. I2顺时针方向,F沿半径背离圆心向外;
 C. I2逆时针方向,F沿半径指向圆心;
C. I2逆时针方向,F沿半径指向圆心;
D. I2逆时针方向,F沿半径背离圆心向外
[解析]当小线圈中通有如图所示的电流I1时,大线圈内含有小线圈中的内磁场和外磁场,且合磁场方向指向纸里。当小线圈中电流增强时,大线圈内的合磁通会增大,因此大线圈中的磁通要阻碍它的增加,产生的感应电流的磁场方向指向纸外,故大线圈中的感应电流方向沿逆时针方向。当大线圈面积变大时,它包含的小线圈的外磁通会变大,从而可以抵消小线圈内部的磁通,故可以阻碍大线圈内磁通量的增加,故大线圈面积要变大,它受到的安培力F应背离圆心向外,如图所示。故本题答案选D。
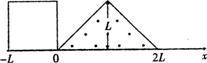 [例3]如图所示,等腰三角形内分布有垂直于纸面向外的匀强磁场,它的底边在x轴上且长为2L,高为L。纸面内一边长为L的正方形导线框沿x轴正方向做匀速直线运动穿过匀强磁场区域,在t=0时刻恰好位于图中所示的位置。以顺时针方向为导线框中电流的正方向,在下面四幅图中能够正确表示电流-位移(I-x)关系的是
( )
[例3]如图所示,等腰三角形内分布有垂直于纸面向外的匀强磁场,它的底边在x轴上且长为2L,高为L。纸面内一边长为L的正方形导线框沿x轴正方向做匀速直线运动穿过匀强磁场区域,在t=0时刻恰好位于图中所示的位置。以顺时针方向为导线框中电流的正方向,在下面四幅图中能够正确表示电流-位移(I-x)关系的是
( )
[解析]线圈向x轴正方向运动L位移的过程中,有效切割长度均匀增加;在位移大于L且小于2L的过程中,线圈右边有效切割长度均匀减小,线圈左边有效切割长度均匀增加,因此整个线圈有效切割长度减小,且变化率为前一段时间的两倍;在位移大于2L且小于3L的过程中,与第一段运动中线圈产生的感应电流等大反向,故A对。

[例4]两根相距为L的足够 长的金属直角导轨如图所示放置,它们各有一边在同一水平内,另一边垂直于水平面。质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路,杆与导轨之间的动摩擦因数均为μ,导轨电阻不计,回路总电阻为2R。整个装置处于磁感应强度大小为B,方向竖直向上的匀强磁场中。当ab杆在平行于水平导轨的拉力F作用下以速度V1沿导轨匀速运动时,cd杆也正好以速度V2向下匀速运动。重力加速度为g。以下说法正确的是 ( )
长的金属直角导轨如图所示放置,它们各有一边在同一水平内,另一边垂直于水平面。质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路,杆与导轨之间的动摩擦因数均为μ,导轨电阻不计,回路总电阻为2R。整个装置处于磁感应强度大小为B,方向竖直向上的匀强磁场中。当ab杆在平行于水平导轨的拉力F作用下以速度V1沿导轨匀速运动时,cd杆也正好以速度V2向下匀速运动。重力加速度为g。以下说法正确的是 ( )
A.ab杆所受拉力F的大小为μmg+ ; B.cd杆所受摩擦力为零;
; B.cd杆所受摩擦力为零;
C.回路中的电流强度为 ; D.μ与V1大小的关系为μ=
; D.μ与V1大小的关系为μ=
[解析] cd杆的速度方向与磁感应强度平行,只有ab杆运动使回路内的磁通量发生变化。根据闭合电路的欧姆定律及法拉第电磁感应定律

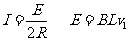
则回路中电流 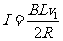
ab杆和cd受力分别如图甲、乙所示。
由图甲可知:水平受力平衡 
竖直受力平衡 
又
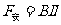
由以上各式可得拉力 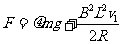
由图乙可知,水平受力平衡
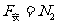 , 竖直受力平衡
, 竖直受力平衡 
故 杆与导轨之间的动摩擦因数
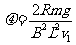
 [例5]如图所示,水平放置的平行导轨上连有电阻R,处于竖直方向的匀强磁场中.现由静止开始用力拉垂直导轨放置的金属棒ab向右运动.若拉力的大小恒定,经过一段时间后棒的速度为v,加速度为a1,最终速度可达3v。若拉力的功率恒定,经过一段时间后棒的速度为v,加速度为a2,最终速度仍可达3v。求a1和a2之比。
[例5]如图所示,水平放置的平行导轨上连有电阻R,处于竖直方向的匀强磁场中.现由静止开始用力拉垂直导轨放置的金属棒ab向右运动.若拉力的大小恒定,经过一段时间后棒的速度为v,加速度为a1,最终速度可达3v。若拉力的功率恒定,经过一段时间后棒的速度为v,加速度为a2,最终速度仍可达3v。求a1和a2之比。
[解析]设磁场的磁感应强度为B,ab棒的长度为L,质量为m. 金属棒运动时感应电动势为 E=BLv,回路中的电流I= ,则金属棒所受安培力
,则金属棒所受安培力 .
.
用恒力时,设恒力的大小为F,当棒的速度为v,加速度为a1时,由牛顿第二定律得:F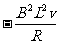 =ma1
=ma1
达到最终速度时,由平衡条件得: F=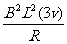
则得 a1=
力的功率恒定时,设力的功率为P,当棒的速度为v,加速度为a2时,由牛顿第二定律得:

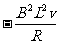 =ma2
=ma2
 达到最终速度时,由平衡条件得:
达到最终速度时,由平衡条件得: =
=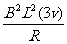
解得:a2=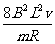
故 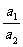 =
=
[例6]如图所示,轻绳绕过轻滑轮连接着边长为L的正方形导线框A1和物块A2,线框A1的电阻为R,质量为M,物块A2的质量为m(M>m),两匀强磁场区域I、II的高度也为L,磁感应强度均为B,方向水平与线框平面垂直。线框ab边距磁场边界高度为h。开始时各段绳都处于伸直状态,把它们由静止释放,ab边刚穿过两磁场的分界线CC进入磁场II时线框做匀速运动。求:
(1)ab边刚进入磁场I时线框A1的速度v1;
(2)ab边进入磁场II后线框A1所受重力的功率P;
(3)从ab边刚进入磁场II到ab边刚穿出磁场II的过程中,线框中产生的焦耳热Q.
[解析](1)由机械能守恒定律,有: ①
①
解得: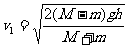 ②
②
(2)设线框ab边进入磁场II时速度为 ,则线框中产生的电动势:
,则线框中产生的电动势:
 ③
③
线框中的电流 ④
④
线框受到的安培力 ⑤
⑤
设绳对A1、A2的拉力大小为T则:
对A1:T+F=Mg ⑥
对A2:T=mg ⑦
联立⑤⑥⑦解得: ⑧
⑧
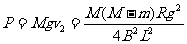 ⑨
⑨
(3)从ab边刚进入磁场II到ab边刚穿出磁场II的此过程中线框一直做匀速运动,根据能量守恒得: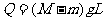 ⑩
⑩
[例7]如图所示,光滑水平面停放一小车,车上固定一边长为L=0.5m的正方形金属线框abcd,金属框的总电阻R=0.25Ω,小车与金属框的总质量m=0.5kg。在小车的右侧,有一宽度大于金属线框边长,具有理想边界的匀强磁场,磁感应强度B=1.0T,方向水平且与线框平面垂直。现给小车一水平速度使其向右运动并能穿过磁场,当车上线框的ab边刚进入磁场时,测得小车加速度a=10m/s2。求:
(1)金属框刚进入磁场时,小车的速度为多大?
(2)从金属框刚要进入磁场开始,到其完全离开磁场,线框中产生的焦耳热为多少?
 解析:(1)由于明确了线框的ab边刚进入磁场时小车的加速度,可以通过其受力情况列方程求解.
解析:(1)由于明确了线框的ab边刚进入磁场时小车的加速度,可以通过其受力情况列方程求解.
设小车初速度为v0,则线框刚进入磁场时,ab边由于切割磁感线产生的电动势为: E=BLv0………………①
回路中的电流:I= ……………②
……………②
根据牛顿定律:BIL=ma……………………③
由以上三式可解得:v0=5m/s
(2)在求得金属框刚进入磁场时,小车的速度后,为了求得从金属框刚要进入磁场,到其完全离开磁场所产生的焦耳热,关键在于求出小车完全离开磁场时的速度.
设线框全部进入磁场时小车速度为v1,进入过程平均电流为 ,所用时间为△t,则
,所用时间为△t,则
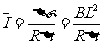 ………………④
………………④
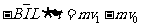 ………………⑤
………………⑤
解得:v1=4m/s
设线框离开磁场时小车速度为v2,进入过程平均电流为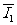 ,所用时间为△t1,则:
,所用时间为△t1,则:
 ………………⑥
………………⑥
 ……………⑦
……………⑦
解得:v2=3m/s
线框从进入到离开产生的焦耳热应等于系统损失的机械能,即:
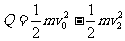 =4.0J
=4.0J
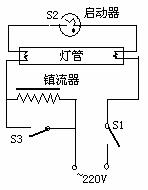
[例8]如图所示是日光灯的结构示意图,若按图示的电路连接,关于日光灯的发光情况,下列叙述中正确的是 ( )
A、 S1接通,S2、S3断开,日光灯就能正常发光;
B、 S1 、S2接通, S3断开,日光灯就能正常发光;
C、 S3断开,接通S1 、S2后,再断开S2,日光灯就能正常发光;
D、当日光灯正常发光后,再接通S3,日光灯仍然能正常发光。
[解析]日光灯的启动利用的是线圈自感现象,其正常的电路图如下,其原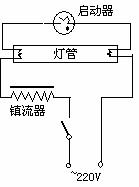 理不再赘述。对选项A,此时是电源电压直接接在灯管两端,达不到灯管启动的高压值,日光灯不能发光;对选项B,将造成灯丝两端短路,电压为零,日光灯同样不能发光;对选项D,当日光灯正常发光后,再接通S3,则镇流器被短路,灯管两端电压过高,造成灯管损坏。当接通S1后,电源电压加在启动器的两极之间,由于热膨胀,S2被接通,使得镇流器中有电流通过,此时启动器中的氖气停止放电,电路自动断开;由于自感的作用,镇流器中产生很大的自感电动势,和原电压加在一起,形成瞬时高压,进而使气体电离,日光灯正常发光,故正确选项为C。
理不再赘述。对选项A,此时是电源电压直接接在灯管两端,达不到灯管启动的高压值,日光灯不能发光;对选项B,将造成灯丝两端短路,电压为零,日光灯同样不能发光;对选项D,当日光灯正常发光后,再接通S3,则镇流器被短路,灯管两端电压过高,造成灯管损坏。当接通S1后,电源电压加在启动器的两极之间,由于热膨胀,S2被接通,使得镇流器中有电流通过,此时启动器中的氖气停止放电,电路自动断开;由于自感的作用,镇流器中产生很大的自感电动势,和原电压加在一起,形成瞬时高压,进而使气体电离,日光灯正常发光,故正确选项为C。
[专题演练]
3、理解楞次定律的内涵,其关键之处在于对“阻碍”二字的理解,这里的阻碍有两层含义,一是感应电流磁场阻碍了原磁场的变化,二是磁场对感应电流的作用力阻碍了导体与磁场的相对运动,这两种表述实质上是等价的。
楞次定律的第二种表述是,感应电流产生的效果,总要反抗引起感应电流的原因,它反映了感应电流产生的机械效果--反抗。由楞次定律可知,感应电流的“效果”总是反抗引起感应电流的“原因”,深刻理解“反抗”的含义.据“反抗”原则,可直接对运动趋势作出判断,更简捷、迅速.
一般判断机械效果宜用第二种表述形式,应用这种表述形式判断机械效果的步骤是,先找出引起感应电流的原因(如磁通量变化、相对运动等),再来确定阻碍方式(如阻碍磁通量变化,阻碍相对运动等)。
2、楞次定律的基本内容是:感应电流的磁场总是阻碍引起感应电流的磁通量的变化,这就是楞次定律.楞次定律解决的是感应电流的方向问题,感应电流的磁场总是要阻碍引起感应电流的磁通量的变化,而不是阻碍引起感应电流的磁场.“阻碍”不是“相反”,“阻碍”既不是阻碍原磁场,也不是阻碍原来的磁通量,而是指感应电流的磁场阻碍原磁场磁通量的增加或减少。“阻碍”不仅有“反抗”的含义,还有“补偿”的含义,即反抗磁通量的增加,补偿磁通量的减少。“阻碍”不是“阻止”,而只是延缓了原磁通的变化,电路中的磁通量还是在变化的。例如,当原磁通量增加时,虽有感应电流的磁场的阻碍,磁通量还是在增加,只是增加的慢一点而已!
由于此定律所牵涉的物理量和物理规律较多,只有对原磁场方向、原磁通量变化情况、感应电流的磁场方向、以及安培定则和右手螺旋定则进行正确的判定和使用,才能得到正确的感应电流的方向.
1、我们知道,不论用什么方法,只要穿过闭合电路的磁通量发生变化,闭合电路中就有感应电流电流产生,这也是产生感应电流的唯一条件。根据磁通量计算公式 可见,引起磁通量发生变化的原因一般有磁场磁感应强度B变化、闭合回路的面积S变化、夹角
可见,引起磁通量发生变化的原因一般有磁场磁感应强度B变化、闭合回路的面积S变化、夹角 变化等等。这里必须注意是“穿过闭合电路的磁通量发生变化”,因而当某时刻穿过闭合电路的磁通量为零时,电路中仍可能有感应电流。
变化等等。这里必须注意是“穿过闭合电路的磁通量发生变化”,因而当某时刻穿过闭合电路的磁通量为零时,电路中仍可能有感应电流。
电磁感应现象的实质是产生感应电动势,如果回路闭合,则有感应电流;当回路不闭合时,则只有感应电动势,而无感应电流。
25. (本题满分14分,第(1)小题满分3分,第(2)小题满分5分,第(3)小题满分6分)
如图9,矩形ABCD中, ,点E是BC边上的一个动点,联结AE,过点D作
,点E是BC边上的一个动点,联结AE,过点D作 ,垂足为点F .
,垂足为点F .
(1)设 ,
, 的余切值为y,求y关于x的函数解析式;
的余切值为y,求y关于x的函数解析式;
(2)若存在点 ,使得
,使得 ABE 、
ABE 、 ADF与四边形CDFE的面积比是3:4:5,
ADF与四边形CDFE的面积比是3:4:5,
试求矩形ABCD的面积;
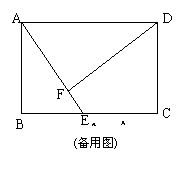
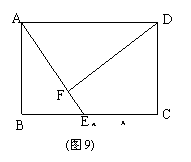 (3)对(2)中求出的矩形ABCD,联结CF,当BE的长为多少时,
(3)对(2)中求出的矩形ABCD,联结CF,当BE的长为多少时, CDF是等腰三角形?
CDF是等腰三角形?
24.(本题满分12分,共3小题,每小题满分各4分)
如图8,已知点A (-2,4) 和点B (1,0)都在抛物线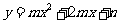 上.
上.
(1)求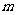 、n;
、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形
 A A′B′B为菱形,求平移后抛物线的表达式;
A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′ 的
交点为点C,试在 轴上找点D,使得以点
轴上找点D,使得以点
B′、C、D为顶点的三角形与 相似.
相似.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com