
23.已知数列{an}的前n项和为Sn,点(an+2,Sn+1)在直线y=4x-5上,其中n∈N*,令bn=an+1-2an,且a1=1.
(1)求数列{bn}的通项公式;
(2)若f(x)=b1x+b2x2+b3x3+…+bnxn,求f ¢(1)的表达式,并比较f ¢(1)与8n2-4n的大小.
22.某大楼共5层,4个人从第一层上电梯,假设每个人都等可能地在每一层下电梯,并且他们下电梯与否相互独立. 又知电梯只在有人下时才停止.
(I)求某乘客在第 层下电梯的概率
层下电梯的概率 ;
;
(Ⅱ)求电梯在第2层停下的概率;
(Ⅲ)求电梯停下的次数 的数学期望.
的数学期望.
(总分40分,加试时间30分钟)
答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷密封线内.解答过程应写在答题卷的相应位置上,在其它地方答题无效。
21.B.选修4-2:矩阵与变换
已知矩阵M=,N=,求直线y=2x+1在矩阵MN的作用下变换所得到的直线方程.
C.选修4-4:坐标系与参数方程
已知⊙C:r=cosq+sinq,直线l:r=.求⊙C上点到直线l距离的最小值.
20.
已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为 ,问:m在什么范围取值时,对于任意的
,问:m在什么范围取值时,对于任意的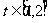 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?
(Ⅲ)当 时,设函数
时,设函数 ,若在区间
,若在区间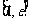 上至少存在一个
上至少存在一个 ,使得
,使得 成立,试求实数p的取值范围.
成立,试求实数p的取值范围.
高三数学试卷 第4页 (共4页)
扬州市2010届高三第二次高考模拟考试样卷(二)
19.
各项均为正数的数列 的前
的前 项和为
项和为 ,
, ;
;
(1)求 ;
;
(2)令 ,
, ,求
,求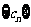 的前
的前 项和
项和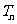 .
.
(3)令 (
( 为常数,
为常数, 且
且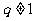 ),
),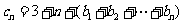 ,
,
是否存在实数对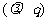 ,使得数列
,使得数列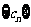 成等比数列?若存在,求出实数对
成等比数列?若存在,求出实数对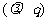 及数列
及数列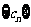
18.已知曲线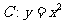 与直线
与直线 交于两点
交于两点 和
和 ,且
,且 .记曲线
.记曲线 在点
在点 和点
和点 之间那一段
之间那一段 与线段
与线段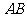 所围成的平面区域(含边界)为
所围成的平面区域(含边界)为 .设点
.设点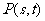 是
是 上的任一点,且点
上的任一点,且点 与点
与点 和点
和点 均不重合.
均不重合.
(1)若点 是线段
是线段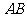 的中点,试求线段
的中点,试求线段 的中点
的中点 的轨迹方程;
的轨迹方程;
(2)若曲线 与
与 有公共点,试求
有公共点,试求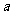 的最小值.
的最小值.
17.已知 ,函数
,函数 .
.
(Ⅰ)当 时,求使
时,求使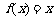 成立的
成立的 的集合;
的集合;
(Ⅱ)求函数 在区间
在区间 上的最小值.
上的最小值.
高三数学试卷 第3页 (共4页)
16. 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,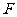 为
为 上的点,且BF⊥平面ACE.
上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)求三棱锥D-AEC的体积;
(3)设M在线段AB上,且满足AM=2MB,试在线段
CE上确定一点N,使得MN∥平面DAE.
15.已知向量 ,函数
,函数 的图像上一个最高点的坐标为
的图像上一个最高点的坐标为 ,与之相邻的一个最低点的坐标
,与之相邻的一个最低点的坐标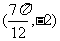 .
.
(1)求 的解析式.
的解析式.
(2)在△ 中,
中, 是角
是角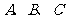 所对的边,且满足
所对的边,且满足 ,求角
,求角 的大小以及
的大小以及 取值范围.
取值范围.
14.定义函数 ,其中
,其中 表示不超过
表示不超过 的最大整数,如:
的最大整数,如: ,当
,当 时,设函数
时,设函数 的值域为A,记集合A中的元素个数为
的值域为A,记集合A中的元素个数为 ,则式子
,则式子 的最小值 ▲
的最小值 ▲
高三数学试卷 第2页 (共4页)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com