5．某公司招聘员工，面试人数y拟照公式表示拟录取人数，现已知面试人数为60人，则该公司拟录取的人数为　　　 人。

　 　 6．已知米拉等可能地落入如图的示的四边形ABCD内，如果通过大量的实验发现米粒△BCD内的频率稳定在附近，那么点A和点C到直线BD的距离之比约为　 　　　。

4．在△ABC中，AB=2，D是AC的中点，若=　　　　 。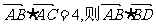

3．已知i是虚数单位，计算：=　　　　　 。

2．命题：“”的否定是　　　　 。

1．已知集合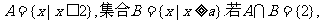则实数a=　　　 。

24．解：(1)四边形ABCE是菱形。　　　　　　 　　　　　　……………………1分

∵△ECD是由△ABC沿BC平移得到的，∴EC∥AB，且EC＝AB，

∴四边形ABCE是平行四边形，　　　　　　　 　　……………………3分

又∵AB=BC，∴四边形ABCE是菱形 .　　　 …………………4分

(2)①四边形PQED的面积不发生变化。　 …………………5分

方法一：∵ABCE是菱形，∴AC⊥BE，OC=AC=3，∵BC=5，∴BO=4，

过A作AH⊥BD于H，(如图1).

∵S_△ABC＝BC×AH＝AC×BO，

即：×5×AH＝×6×4，∴AH＝.　　 ……………………6分

[或 ∵∠AHC＝∠BOC＝90°，∠BCA公用，∴△AHC∽△BOC，∴AH:BO＝AC:BC，

即：AH:4＝6:5，∴AH＝.　　　　　 ……………………6分]

由菱形的对称性知，△PBO≌△QEO，∴BP＝QE，

∴S_{四边形PQED}＝(QE+PD)×QR＝(BP+PD)×AH＝BD×AH

　 ＝×10×＝24.　　　　　　　　 ……………………8分

方法二: 由菱形的对称性知，△PBO≌△QEO，∴S_△PBO＝ S_△QEO，…………6分

∵△ECD是由△ABC平移得到得，∴ED∥AC，ED＝AC＝6，

又∵BE⊥AC，∴BE⊥ED，　　　　　　　　　　　　 　　　　……………7分

∴S_{四边形PQED}＝S_△QEO+S_{四边形POED}＝S_△PBO+S_{四边形POED}＝S_△BED

＝×BE×ED＝×8×6＝24.　　　　　　　　　　　　　　　 　……………8分

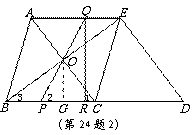
②方法一：如图2，当点P在BC上运动，使△PQR与△COB相似时，

∵∠2是△OBP的外角，∴∠2＞∠3，∴∠2不与∠3对应，∴∠2与∠1对应，

即∠2＝∠1，∴OP=OC=3　　　 　　　　　　　　　　　　　　　……………9分

过O作OG⊥BC于G，则G为PC的中点，△OGC∽△BOC，　 ……………10分

∴CG:CO＝CO:BC，即：CG:3＝3:5，∴CG=，　　　　 ……………11分

∴PB＝BC－PC＝BC－2CG＝5－2×＝.　　　　　　　　 ……………12分

方法二：如图3，当点P在BC上运动，使△PQR与△COB相似时，

∵∠2是△OBP的外角，∴∠2＞∠3，

∴∠2不与∠3对应，∴∠2与∠1对应，　　　　　　　　 ……………9分

∴QR:BO＝PR:OC，即：:4＝PR:3，∴PR＝，　　　 ……………10分

过E作EF⊥BD于F，设PB＝x，则RF=QE=PB=x，

DF＝==，　　　　　　　　　　　 ……………11分

∴BD＝PB+PR+RF+DF＝x++x+＝10，x＝.　　　 ……………12分

方法三: 如图4，若点P在BC上运动，使点R与C重合，

由菱形的对称性知，O为PQ的中点，∴CO是Rt△PCQ斜边上的中线，

∴CO=PO，　　　　　　　　　　　　　　　　　　　　　 ……………9分

∴∠OPC＝∠OCP，此时，Rt△PQR∽Rt△CBO，　　　　 ……………10分

∴PR:CO＝PQ:BC，即PR:3＝6:5，∴PR＝　　　　　　 ……………11分

∴PB＝BC-PR＝5－＝.　　　　　　　　　　　　　　　 ……………12分

23、解：(1)B(1，)(……………2分)

(2)设抛物线的解析式为y=ax(x+a)，代入点B(1, )，得，(……………3分)

因此(……………5分)

(3)如图，抛物线的对称轴是直线x=-1，当点C位于对称轴与线段AB的交点时，△BOC的周长最小. (1分)

设直线AB为y=kx+b.所以，

因此直线AB为，(……………7分)

当x=－1时，，

因此点C的坐标为(－1，)(……………8分).

当x=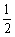－时，△PAB的面积的最大值为，此时.(……………10分)

22、(1)设启动活动前的一个月销售给农户的 I型冰箱和 II型冰箱分别为台．　

根据题意得(……………2分)

解得(……………3分)

∴启动活动前的一个月销售给农户的 I型冰箱和 II型冰箱分别为560台和400台．

(2)I型冰箱政府补贴金额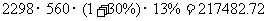：元，(…………4分)　

II　 型冰箱政府补贴金额：元．(……………6分)　　

∴启动活动后第一个月两种型号的冰箱政府一共补贴金额：

元 ．(……………9分)

答：启动活动后第一个月两种型号的冰箱政府一共约补贴农户元．(……………10分)

20、(1)，；(……………2分)

(2)解法1：∵直线经过坐标原点，

∴设所求函数的关系式是，

又点的坐标为(1，2)，

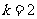∴．……………3分

∴直线所对应的函数关系式是．(……………4分)

解法 2：设所求函数的关系式是

则由题意得：

解这个方程组，得

……………6分

∴直线所对应的函数关系式是．

(3)利用直尺和圆规，作线段关于直线的

对称图形，如图所示．(……………8分)

21、(1)当r=3时，圆O与坐标轴有1个交点；(……………2分)

(2)当3<r<4时，圆O与坐标轴有2个交点；(……………2分)

　　 (3)当r=4时，圆O与坐标轴有3个交点；(…………… 2分)

(4)当r>4时，圆O与坐标轴有4个交点；(……………2分)

19、解：(1)略；(………2分)(2)40，20；(……………2分)(3)600．(……………2分)