
21.(本小题满分12分)
已知椭圆 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线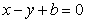 是抛物线
是抛物线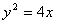 的一条切线.
的一条切线.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.
的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.
20.(本小题满分12分)
已知函数 ,若
,若 的单调减区间为
的单调减区间为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)对任意的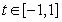 ,关于
,关于 的方程
的方程 总有实根,求实数
总有实根,求实数 的取值范围.
的取值范围.
19.(本小题满分12分)
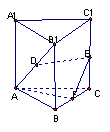
已知直三棱柱 中,
中, 为等腰直角三角形,
为等腰直角三角形,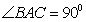 ,
,
 且
且 ,
, 分别为
分别为 的中点,
的中点,
(Ⅰ)求证: //平面
//平面 ;
;
(Ⅱ)求证: 平面
平面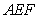 ;
;
(Ⅲ)求点 到平面
到平面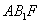 的距离.
的距离.
18.(本小题满分12分)
某商场举行抽奖活动,从装有编号0,1,2,3四个小球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖.
(Ⅰ)求中三等奖的概率;
(Ⅱ)求中奖的概率.
17.(本小题满分10分)
 中,
中, 分别是
分别是 的对边,且
的对边,且 .
.
(Ⅰ)求 ;
;
(Ⅱ)若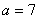 ,
, 的面积为
的面积为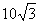 ,求
,求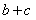 的值.
的值.
16.已知正方体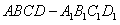 的棱长为1,E为棱
的棱长为1,E为棱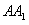 的中点,一直线过E点与异面直线
的中点,一直线过E点与异面直线 ,
, 分别相交于M,N两点,则线段MN的长等于
.
分别相交于M,N两点,则线段MN的长等于
.
15. 已知实数列
已知实数列 中,
中, ,
,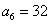 ,
, ,把数列
,把数列 的各项排成
的各项排成
如图所示的三角形状,记 为第
为第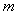 行从左起第
行从左起第 个数,
个数,
则A(12,5)=
. 
14.已知定点 ,
, 是坐标原点,点
是坐标原点,点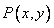 满足
满足 ,则
,则 的最大值为
.
的最大值为
. 
13. 如图,平面上一长
如图,平面上一长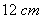 ,宽
,宽 的矩形
的矩形 内有一
内有一
半径为 的圆(圆心在矩形对角线交点处). 把一枚半径
的圆(圆心在矩形对角线交点处). 把一枚半径
 的硬币任意掷在矩形内(硬币完全落在矩形内),则硬币
的硬币任意掷在矩形内(硬币完全落在矩形内),则硬币
不与该圆相碰的概率为
. 
11. 已知函数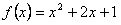 ,若存在实数
,若存在实数 ,当任意
,当任意 时,
时,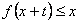 恒成立,则实数
恒成立,则实数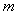 的最大值为( )
的最大值为( )
A. 5
B. 4
C. 3
D. 2
12若双曲线 的一个焦点到一条渐近线的距离等于焦距的
的一个焦点到一条渐近线的距离等于焦距的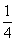 ,则该双曲线的离心率是( )
,则该双曲线的离心率是( ) 
A. B.
B.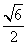 C.
C.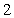 D.
D.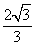

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com