
20.(14分)设函数f(x)=ax-,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
(1)求f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
19. (本小题满分14分)
已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(,0).
(1)求双曲线C的方程;
(2)若直线:y=kx+m(k≠0,m≠0)与双曲线C交于不同的两点M、N,且线段MN的垂直平分线过点A(0,-1),求实数m的取值范围.
18. (14分)如图,在四棱锥P-ABCD中,底面ABCD是边长为
(14分)如图,在四棱锥P-ABCD中,底面ABCD是边长为 的正方形,E为PC的中点,PB=PD.
的正方形,E为PC的中点,PB=PD.
(1)证明:BD ⊥平面PAC.
(2)若PA=PC=2,求三棱锥E-BCD的体积。
11.若 , 则
, 则 的最小值为 ;
的最小值为 ;
12.在△ABC中,三个内角A,B,C对应的边分别为 ,则
,则 的值为 ;
的值为 ;
13. 已知各顶点都在一个球面上的正四棱柱的高为2,这个球的表面积为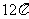 ,则这个正四棱 柱的体积为 ;
,则这个正四棱 柱的体积为 ;
(下面14,15题为选做题)
 14.已知直线的极坐标方程为
14.已知直线的极坐标方程为 ,则点
,则点 到这条直线的距离为 ;
到这条直线的距离为 ;
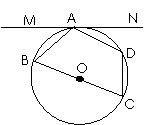
15.如图,四边形ABCD内接于圆O,BC是直径,MN切该圆于A ,
∠MAB=25°,则∠D的度数为 .
三.解答题(写出必要的解题步骤,共80分)
16.(12分)已知:0<α<<β<π,cos(β-)=,sin(α+β)=.
(1)求sin2β的值;
(2)求cos(α+)的值.
17.(12分)
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为a,第二次出现
的点数为b.设复数z=a+bi.
(1)求事件“z-3i为实数”的概率;
(2)求事件“复数z在复平面内的对应点(a,b)满足(a-2)2+b2≤9”的概率.
10.如图 ,直角三角形
,直角三角形 的直角边
的直角边 ,记
,记 ,则数列
,则数列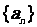 的通项公式为
( )
的通项公式为
( )
 .
.  B.
B. 
C.  D.
D. 
二填空题(每题5分,14,15题两题只选做其中一题,共20分)
9.
 下列选项错误的是
( )
下列选项错误的是
( )
A.命题 的否定是
的否定是
B.命题“所有的等边三角形都是等腰三角形”的否定是“有一个等边三角形不是等腰三角形”;
C.命题“若 ,则
,则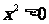 ”的逆命题是“若
”的逆命题是“若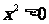 ,则
,则 ”;
”;
D. 命题“若 ,则
,则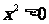 ”的否命题是“若
”的否命题是“若 ,则
,则 ”;
”;
8.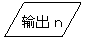
 右边程序框图最后一次输出的n的值为
( )
右边程序框图最后一次输出的n的值为
( )
A. 55 B. 56 C. 57 D.58
7.经过圆 的圆心,且与直线
的圆心,且与直线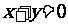 垂直的直线方程为
( )
垂直的直线方程为
( )

|



|

 A.
A.  B.
B. 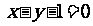
|
|
 C.
C. 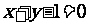 D.
D. 
6.不等式组 表示的平面区域的面积为
( )
表示的平面区域的面积为
( )
A.  B.
B. C.
C. D.
D.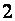
5.已知函数 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则
,则
A. 1 B. -1 C. 2 D. -2 ( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com