
17.(本小题满分12分)在△ABC中,已知AB= ,BC=1,cosC=
,BC=1,cosC=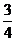 .
.
(Ⅰ)求sinA的值;(Ⅱ)求 的值.
的值.
解:(Ⅰ)因为cosC=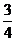 ,则sinC=
,则sinC=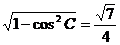 .
(3分)
.
(3分)
据正弦定理,有 ,所以sinA=
,所以sinA= .
(6分)
.
(6分)
(Ⅱ)由余弦定理,得 .
.
设AC=b,则 ,即
,即 .
(8分)
.
(8分)
解得b=2或b= (舍去),AC=2.
(9分)
(舍去),AC=2.
(9分)
故 .
(12分)
.
(12分)
18 .(本题满分12分)某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2.4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元.
.(本题满分12分)某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2.4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元.
(Ⅰ)求下表中的 值;
值;
(Ⅱ)若以频率作为概率,①求购买该品牌汽车的3位顾客中,至多有1位采用3期付款的概率;
②若用 表示该4S店售出一辆汽车的利润.求
表示该4S店售出一辆汽车的利润.求 的分布列及数学期望
的分布列及数学期望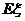 .
.
|
付款方式 |
分1期 |
分2期 |
分3期 |
分4期 |
分5期 |
|
频 数 |
40 |
20 |
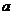 |
10 |
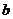 |
解:(Ⅰ)由 得
得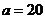
∵ ∴
∴ (2分)
(2分)
(Ⅱ)①∵采用3期付款的概率0.2,
∴购买该品牌汽车的3位顾客中至多有1位采用3期付款的概率为 =
= (7分)
(7分)
②∵ 的可能取值为:1,1.5,2(单位万元)
的可能取值为:1,1.5,2(单位万元)
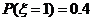 ,
, ,
, (10分)
(10分)
 |
1 |
1.5 |
2 |
|
P |
0.4 |
0.4 |
0.2 |
∴ 的分布列为:
的分布列为:
 ∴
∴ 的数学期望
的数学期望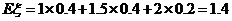 (万元) (12分)
(万元) (12分)
16.已知函数 .对于下列命题:①函数
.对于下列命题:①函数 是定义在R上的单调函数;②函数
是定义在R上的单调函数;②函数 是周期函数;③函数
是周期函数;③函数 的图象是轴对称图形;④方程
的图象是轴对称图形;④方程 在区间
在区间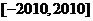 上的根的个数是4021.
上的根的个数是4021.
其中真命题的序号是 .(写出所有真命题的序号)
答案③④ 由 是
是 的零点,知④对;又
的零点,知④对;又 不恒等于0,可知
不恒等于0,可知 不单调,①错;
不单调,①错;  不是周期函数,
不是周期函数,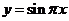 是周期函数,
是周期函数, 不是周期函数,②错;
不是周期函数,②错;
 ,
, 的图象关于直线
的图象关于直线 对称,③对。
对称,③对。
15.已知 ,若对任意实数
,若对任意实数 都有
都有 ,则
,则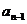 =________
=________
答案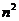
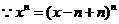 ,
, .
.
14.已知函数 在
在 处连续,则实数
处连续,则实数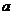 的值为 .
的值为 .
答案1  .
.
13.一个总体依有100个个体,随机编号0,1,2,…,99,依从小到大的编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=8,则在第8组中抽取的号码是_________.
答案:76 依题意,8+8的个位数为6,又在第8组,所以抽取的号码是76.
12.已知映射 .设点
.设点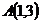 ,
, ,点M 是线段AB上一动点,
,点M 是线段AB上一动点, .当点M在线段AB上从点A开始运动到点B结束时,点M的对应点
.当点M在线段AB上从点A开始运动到点B结束时,点M的对应点 所经过的路线长度为( )
所经过的路线长度为( )
A. B.
B.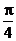 C.
C. D.
D.
答案C 直线AB的方程为x+y=4,设点M(m,n),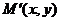 ,则
,则 ,
,
即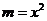 ,
, .因为m+n=4(1≤m≤2),则
.因为m+n=4(1≤m≤2),则 .
.
所以点 的轨迹为一段圆弧,且圆心角为
的轨迹为一段圆弧,且圆心角为 ,所以弧长为
,所以弧长为 ,故选C.
,故选C.
11. 平面内称横坐标为整数的点为“次整点”.过函数
平面内称横坐标为整数的点为“次整点”.过函数 图象上任意两个次整点作直线,则倾斜角大于45°的直线条数为( )
图象上任意两个次整点作直线,则倾斜角大于45°的直线条数为( )
A.10 B.11 C.12 D.13
答案B 如图,设曲线 的次整点分别为
的次整点分别为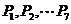 ,过点
,过点
 倾斜角大于4
倾斜角大于4 5°的直线有
5°的直线有 ,过点
,过点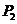 的有
的有 ,
,
过点 有
有 、
、 ,过点
,过点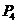 有
有 、
、 、
、 ,过
,过
点 有
有 ,过点
,过点 的有
的有 ,共11条,故选B.
,共11条,故选B.
10.设实数 满足约束条件
满足约束条件 ,若目标函数
,若目标函数
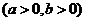 的最大值为12,
的最大值为12,
则 的最小值为( )
的最小值为( )
A. B.
B. C.
C.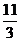 D.4
D.4
答案B 解得 的最优解为(4,6),
的最优解为(4,6),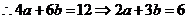 ,
,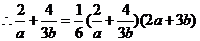
 ,故选B.
,故选B.
9.若长方体 的8个顶点在同一个球面上,且
的8个顶点在同一个球面上,且 ,
,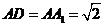 ,则顶点A、B间的球面距离是( )
,则顶点A、B间的球面距离是( )
A. B.
B. C.
C. D.
D.
答案D  ,
, ,
, A、B间的球面距离是
A、B间的球面距离是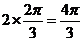 ,故选D.
,故选D.
8.在△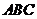 中,三内角
中,三内角 、
、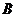 、
、 所对的边分别为
所对的边分别为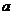 、
、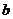 、
、 ,如果
,如果 ,那么( )
,那么( )
A. B.
B.
C . D.
D.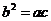
答案D 
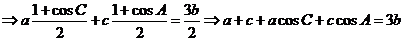 ,
,
 ,
,
 ,故选D.
,故选D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com