
1. 已知全集U和集合A,B如图所示,则 ▲
.
▲
.
23.已知抛物线 ,过其对称轴上一点
,过其对称轴上一点 作一直线交抛物线于
作一直线交抛物线于 两点,若
两点,若 ,求
,求 的斜率.
的斜率.
22.在2009年春运期间,一名大学生要从南京回到徐州老家有两种选择,即坐火车或汽车.已知该大学生先去买火车票的概率是先去买汽车票概率的3倍,汽车票随时都能买到.若先去买火车票,则买到火车票的概率为0.6,买不到火车票,再去买汽车票.
(1)求这名大学生先去买火车票的概率;
(2)若火车票的价格为120元,汽车票的价格为280元,设该大学生购买车票所花费钱数为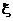 ,求
,求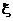 的数学期望值.
的数学期望值.
22.[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
21.[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
A.选修4-1:几何证明选讲
 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
⊙O交直线OB于E、D,连结EC、CD.
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED=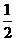 ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
B.选修4-2:矩阵与变换
为了保证信息安全传输,设计一种密码系统,其加密、解密原理如下图:

现在加密方式为:把发送的数字信息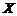 ,写为“
,写为“ ”的形式,先左乘矩阵
”的形式,先左乘矩阵 ,再左乘矩阵
,再左乘矩阵 ,得到密文
,得到密文 ,现在已知接收方得到的密文是
,现在已知接收方得到的密文是 ,试破解该密码.
,试破解该密码.
C.选修4-4:坐标系与参数方程
以直角坐标系的原点O为极点,x轴的正半轴为极轴.已知点P的直角坐标为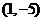 ,
,
点M的极坐标为 .若直线l过点P,且倾斜角为
.若直线l过点P,且倾斜角为 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.
(1)求直线l的参数方程和圆C的极坐标方程;
(2)试判定直线l和圆C的位置关系.
D.选修4-5:不等式选讲
设 均为实数,求
均为实数,求 的最大值.
的最大值.
20.(本小题共16分)已知数列 ,
, 满足
满足 ,
, ,
,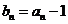 数列
数列 的前
的前 项和为
项和为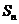 ,
, .
.
(1)求证:数列 为等差数列,并求通项
为等差数列,并求通项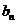 ;
;
(2)求证: ;
;
(3)求证:当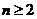 时,
时, .
.
数学附加题
19.(本小题共16分)已知函数 在
在 上是增函数.
上是增函数.
(1)求实数a的取值范围;
(2)在(1)的结论下,设 ,求函数
,求函数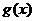 的最小值.
的最小值.
18.(本小题共16分)
设 .
.
(1)证明:对任意 ,当
,当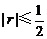 时,
时, ;
;
(2)证明:当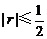 ,
, 对任意
对任意 和自然数
和自然数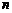
 都有
都有 .
.
17.(本小题共14分)椭圆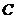 :
: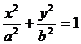
 的一个焦点
的一个焦点 ,右准线方程
,右准线方程 .
.
(1)求椭圆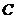 的方程;
的方程;
(2)若 为右准线上一点,
为右准线上一点, 为椭圆
为椭圆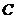 的左顶点,连结
的左顶点,连结 交椭圆于点
交椭圆于点 ,求
,求 的取值范围;
的取值范围;
(3)设圆Q: 与椭圆
与椭圆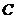 有且只有一个公共点,过椭圆
有且只有一个公共点,过椭圆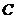 上一点
上一点 作圆Q的切线
作圆Q的切线 、
、 ,切点为
,切点为 ,求
,求 的最大值.
的最大值.
16. (本小题共14分)
(本小题共14分)
如图所示,在直三棱柱 中,
中, ,
, 平面
平面 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)设 是
是 上一点,试确定
上一点,试确定 的位置使平面
的位置使平面
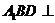 平面
平面 ,并说明理由.
,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com