
19.(14分) (1) 已知某圆的极坐标方程为:ρ2 -4ρcos(θ-)+6=0.将极坐标方程化为普通方程;并选择恰当的参数写出它的参数方程。
(2) 已知二阶矩阵M有特征值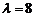 及对应的一个特征向量
及对应的一个特征向量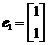 , 且矩阵M对应的变换将点(−1, 2)变换成(−2, 4)。求矩阵M的另一个特征值及对应的一个特征向量e2的坐标之间的关系。
, 且矩阵M对应的变换将点(−1, 2)变换成(−2, 4)。求矩阵M的另一个特征值及对应的一个特征向量e2的坐标之间的关系。
18.(14分)在一个盒子中,放有标号分别为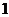 ,
,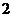 ,
,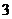 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为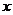 ,
,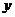 ,记
,记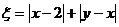 .
.
(1)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量 的分布列和数学期望.
的分布列和数学期望.
17.(16分)已知下表中的对数值有且只有两个是错误的。
|
x |
1.5 |
3 |
5 |
6 |
7 |
8 |
9 |
14 |
27 |
|
lgx |
3a−b+c |
2a−b |
a+c |
1+a−b−c |
2(a+c) |
3(1−a−c) |
2(2a−b) |
1−a+2b |
3(2a−b) |
(1)假设上表中lg3=2a−b与lg5=a+c都是正确的,试判断lg6=1+a−b−c是否正确,给出判断过程;
(2) 求证lg3的对数值是正确的;
(3)试将两个错误的对数值均指出来, 并加以改正(不要求证明)
16.(16分)某公司为了获得更大的收益,每年要投入一定的资金用于广告促销.经调查发现投入广告费t(百万元),可增加销售额约为-t2+5t(百万元)(0≤t≤5).
(1)若该公司将当年的广告费控制在3百万元之内,则应投入多少广告费,才能使该公司由此获得的收益最大?
(2)现该公司准备共投入3百万元,分别用于广告促销和技术改造.经预测,每投入技术改造费x(百万元),可增加的销售额约为-x3+x2+3x(百万元).请设计一个资金分配方案,使该公司由此获得的收益最大?(注:收益=销售额-投放).
15.(14分)已知集合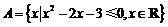
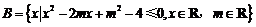 .
.
(Ⅰ)若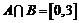 ,求实数
,求实数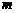 的值;
的值;
(Ⅱ)若AÍCRB,求实数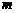 的取值范围.
的取值范围.
14.在实数集R中定义一种运算“*”,具有性质:①对任意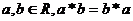 ;
;
②对任意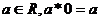 ;
;
③对任意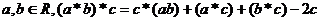 ,
,
则函数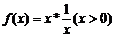 的最小值为
的最小值为
13.已知f (x)是以2为周期的偶函数,当x∈[0, 1]时,f (x)= x,且在[−1,3]内,
函数g(x)=f (x)−kx−k−1有4个零点,则实数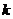 得取值范围是 ______ .
得取值范围是 ______ .
12.已知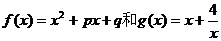 都是定义在
都是定义在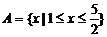 上的函数,对任意的
上的函数,对任意的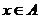 ,存在常数
,存在常数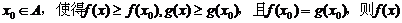 在A上的最大值为_____
在A上的最大值为_____
11.对大于1的自然数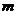 的三次幂可用奇数进行以下方式的“分裂”:23 33 43 … 仿此,若m3的“分裂数”中有一个是59, 则
的三次幂可用奇数进行以下方式的“分裂”:23 33 43 … 仿此,若m3的“分裂数”中有一个是59, 则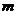 的值为 .
的值为 .
10.在平面直角坐标系xoy中,直线l的参数方程为(t∈R), 圆C的参数方程为(θ∈[0,2π]),则直线l截圆C所得的弦长为__________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com