
6.已知平面向量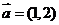 ,
, ,则
,则 与
与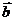 夹角的余弦值
夹角的余弦值
为 ▲ .
7. 把分别写有“灰”、“太”、“狼”的三张卡片随意排成一排,则能使
卡片排成的顺序从左向右或从右向左都可以念为“灰太狼”的概率
是 ▲ .(用分数表示)
5.函数 在
在 上的单调递减区间为 ▲ .
上的单调递减区间为 ▲ .
4.命题“ ,
, ”的否定是 ▲ .
”的否定是 ▲ .
3.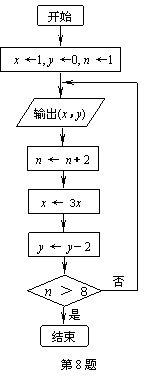 直线
直线 经过点
经过点 ,且与直线
,且与直线 垂直,则
垂直,则 的方程
的方程
是 ▲ .
2.若复数 (
( 是虚数单位,
是虚数单位, )是纯虚数,则
)是纯虚数,则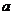 = ▲ .
= ▲ .
1.设集合 ,
, ,则
,则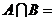 ▲ .
▲ .
20.函数 是
是 上的增函数.
上的增函数.
(Ⅰ)求正实数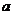 的取值范围;
的取值范围;
(Ⅱ)若函数 对定义域内的任意x值恒成立的所有常数M中,我们把M的最大值M=
对定义域内的任意x值恒成立的所有常数M中,我们把M的最大值M=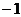 叫做
叫做 的下确界,若函数
的下确界,若函数 的定义域为
的定义域为 ,根据所给函数g(x)的下确界的定义,求出当a=1时函数f(x)的下确界。
,根据所给函数g(x)的下确界的定义,求出当a=1时函数f(x)的下确界。
(Ⅲ)设 ,求证:
,求证:
解:(1) ……2分
……2分
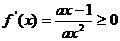 对
对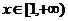 恒成立,……………3分
恒成立,……………3分
 对
对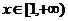 恒成立
恒成立
又
 为所求.…………………………5分
为所求.…………………………5分
(2)由(1)可知a=1时,函数f(x)是定义域 上的增函数,故
上的增函数,故 6分
6分
 …………………9分
…………………9分
 当a=1时函数f(x)的下确界为0. …………………10分
当a=1时函数f(x)的下确界为0. …………………10分
(3)取 ,
, ,…………………12分
,…………………12分
由(1)知 在
在 上是增函数,
上是增函数, …………14分
…………14分
 ,即
,即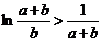 ………………16分
………………16分
19.点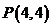 ,圆
,圆 :
: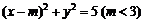 与椭圆
与椭圆 :
: 有一个公共点
有一个公共点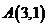 ,
, 分别是椭圆的左、右焦点,直线
分别是椭圆的左、右焦点,直线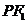 与圆
与圆 相切.
相切.
(Ⅰ)求 的值与椭圆
的值与椭圆 的方程;
的方程;
(Ⅱ)设 为椭圆
为椭圆 上的一个动点,求
上的一个动点,求 的取值范围.
的取值范围.

解:(Ⅰ)点A代入圆C方程,
得 .
.
∵m<3,∴m=1. …… 2分
圆C: .
.
设直线PF1的斜率为k,
则PF1: ,
,
即 .
.
∵直线PF1与圆C相切,
∴ .
.
解得 . …………… 4分
. …………… 4分
当k= 时,直线PF1与x轴的交点横坐标为
时,直线PF1与x轴的交点横坐标为 ,不合题意,舍去.
,不合题意,舍去.
当k= 时,直线PF1与x轴的交点横坐标为-4,
时,直线PF1与x轴的交点横坐标为-4,
∴c=4.F1(-4,0),F2(4,0). …………………… 6分
2a=AF1+AF2= ,
, ,a2=18,b2=2.
,a2=18,b2=2.
椭圆E的方程为: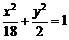 .
…………………… 8分2
.
…………………… 8分2
(Ⅱ) ,设Q(x,y),
,设Q(x,y), ,
,
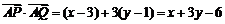 .
…………………… 12分
.
…………………… 12分
∵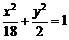 ,即
,即 ,
,
而 ,∴-18≤6xy≤18.
,∴-18≤6xy≤18.
则 的取值范围是[0,36]. ……… 15分
的取值范围是[0,36]. ……… 15分
 的取值范围是[-6,6].
-------16分
的取值范围是[-6,6].
-------16分
15.已知复数 ,
, ,且
,且 ,其中
,其中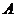 、
、 、
、 为△ABC的内角,
为△ABC的内角,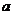 、
、 、
、 为角
为角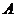 、
、 、
、 所对的边.
所对的边.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ) 若 ,求△ABC的面积.
,求△ABC的面积.
解:(Ⅰ)∵
∴ ----①,
----①,  ----② -----------2分
----② -----------2分
由①得 ----------③ -----------3分
----------③ -----------3分
在△ABC中,由正弦定理得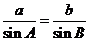 =
=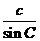 ,
,
设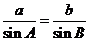
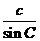 =
=
则 ,代入③得
,代入③得
 -----------------------4分
-----------------------4分
 -----------------5分
-----------------5分
∵  ∴
∴
∴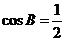 ,
,
∵ ∴
∴ --------------7分
--------------7分
(Ⅱ) ∵ ,由余弦定理得
,由余弦定理得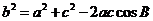

 ,--④----------------------------10分
,--④----------------------------10分
由②得 ------------⑤
------------⑤
由④⑤得 ,--------------------------------------12分
,--------------------------------------12分
∴ =
=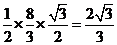 .-------------------------14分
.-------------------------14分
16. (本小题满分13分)
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为 的菱形,
的菱形,
∠ACC1为锐角,侧面ABB1A1⊥侧面AA1C1C,且A1B=AB=AC=1.
(Ⅰ)求证:AA1⊥BC1;
(Ⅱ) 求三棱锥A1-ABC的体积.
(1)证明 : 因为四边形AA1C1C是菱形,所以有AA1=A1C1=C1C=CA=1.
 从而知△AA1B是等边三角形.
------------2分
从而知△AA1B是等边三角形.
------------2分
设D是AA1的中点、连结BD,C1D,
则BD⊥AA1,由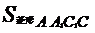 =
=
知C1到AA1的距离为 ∠AA1C1=60°,
∠AA1C1=60°,
所以△AA1C1是等边三角形,-----4分
且C1D⊥AA1,所以AA1⊥平面BC1D. ------------6分
又BC1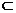 平面BC1D,故AA1⊥BC1. ------------7分
平面BC1D,故AA1⊥BC1. ------------7分
(2) 由(1)知BD⊥AA1,又侧面ABB1A1⊥侧面AA1C1C,所以BD⊥平面AA1C1C,
即B到平面AA1C1C 的距离为BD. --------9分
又 =
=
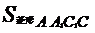
 ,BD=
,BD=
所以 =
= =
=
 ·BD=
·BD= ×
× ×
× =
= ------------13分
------------13分
故三棱锥A1-ABC的体积为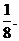 ------14分
------14分
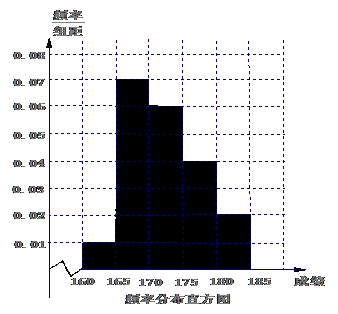
17.某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(Ⅰ)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多
少名学生进入第二轮面试?
 (Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
(Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
 |
5 |
0.050 |
|
第2组 |
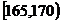 |
① |
0.350 |
|
第3组 |
 |
30 |
② |
|
第4组 |
 |
20 |
0.200 |
|
第5组 |
 |
10 |
0.100 |
|
合计 |
100 |
1.00 |
解:(Ⅰ)由题可知,
第2组的频数为  人, -----1分
人, -----1分
第3组的频率为 ,
-----2分
,
-----2分
频率分布直方图如下: -------5分
(Ⅱ)因为第3、4、5组共有60名学生,所以
 利用分层抽样在60名学生中抽取6名学生,每组分别为:
利用分层抽样在60名学生中抽取6名学生,每组分别为:
第3组: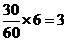 人, ------------ 6分
人, ------------ 6分
第4组: 人, ------------ 7分
人, ------------ 7分
第5组: 人, ------------ 8分
人, ------------ 8分
所以第3、4、5组分别抽取3人、2人、1人。
(Ⅲ)设第3组的3位同学为 ,第4组的2位同学为
,第4组的2位同学为 ,第5组的1位同学为
,第5组的1位同学为 ,
,
则从六位同学中抽两位同学有15种可能如下: 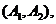
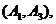

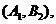
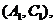


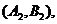

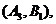




 --
10分
--
10分
其中第4组的2位同学为 至少有一位同学入选的有:
至少有一位同学入选的有: 
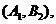

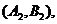
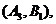



 9中可能, --- 12分
9中可能, --- 12分
所以其中第4组的2位同学为 至少有一位同学入选的概率为
至少有一位同学入选的概率为 -------14分
-------14分
18.已知已知函数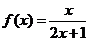 ,数列
,数列 满足
满足 .
.
(Ⅰ)求证:数列 是等差数列;
是等差数列;
(Ⅱ)记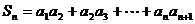 ,试比较
,试比较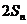 与1的大小.
与1的大小.
解:(Ⅰ)由已知得, , ∴
, ∴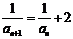 ,即
,即 .
.
∴数列 是首项
是首项 ,公差
,公差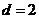 的等差数列. -------6分
的等差数列. -------6分
(Ⅱ) 由(Ⅰ)知 , ∴
, ∴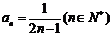 ,-------8分
,-------8分
∴ , -------10分
, -------10分
∴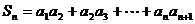


 . -------14分
. -------14分
∴
 , ∴
, ∴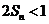 . -------16分
. -------16分
14.已知函数 ,正实数
,正实数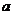 、
、 、
、 满足
满足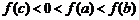 ,若实数
,若实数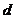 是函数
是函数 的一个零点,那么下列四个判断:①
的一个零点,那么下列四个判断:①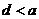 ;②
;②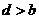 ;③
;③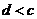 ;④
;④ .其中可能成立的个数为_____ 2
.其中可能成立的个数为_____ 2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com