2.性质：平面截球所得的截面是圆.

(1)球心和球面圆心的连线垂直于截面；

(2)球心到截面的距离d与球的半径R及截面的半径r的关系：

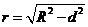
1.定义：半圆以它的直径为旋转轴，旋转所成的曲面叫做球面。球面所围成的几何体叫做球体.

球面是到定点的距离小于或等于定长的点的集合.

过球面上两点的大圆在这两点间劣弧的长叫做两点的球面距离.

地球上的径度是个二面角，纬度是个线面角。

4.棱锥的体积:　 V=Sh，其S是棱锥的底面积，h是高.

3.一般棱锥的性质--定理：

如果棱锥被平行于棱锥底面的平面所截，那么截面和底面相似，并且它们面积的比等于截得的棱锥的高和已知棱锥高的平方比.

2.正棱锥的性质--侧棱、侧面的性质和一些RtΔ

(1)各侧棱相等，各侧面都是全等的等腰三角形.

(2)棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形；棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形.

1.定义：有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫棱锥.

如果一个棱锥的底面是正多边形，并且顶点在底面的射影是底面中心，这样的棱锥叫做正棱锥.

(1) 棱柱的定义：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱.

(2) 棱柱的性质：--侧棱、侧面、横截面、纵截面的性质

①侧棱都相等，侧面都是平行四边形；

②两个底面与平行于底面的截面是全等的多边形；

③过不相邻的两条侧棱的截面是平行四边形.

(3)棱柱的分类：

①按底面多边形的边数分类：三棱柱，四棱柱，…，n棱柱.

②按侧棱与底面的位置关系分类:

(4)特殊的四棱柱:　

四棱柱→ 平行六面体→　 直平行六面体

→长方体→ 正四棱柱 →　 正方体.请在“→”上方添上相应的条件.

(5)长方体对角线定理:

长方体的一条对角线的平方等于一个顶点上三条棱的长的平方和.

(6)棱柱的体积公式:

,是棱柱的底面积,是棱柱的高.

3．了解球、球面的概念, 掌握球的性质及球的表面积、体积公式, 理解球面上两点间距离的概念, 了解与球内接、外切几何问题的解法．

2.会画棱柱、棱锥的直观图，能运用前面所学知识分析论证多面体内的线面关系，并能进行有关角和距离的计算.

1.理解棱柱、棱锥的有关概念，掌握棱柱、棱锥的性质和体积计算；