
22.(本题满分12分)
已知函数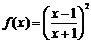 (其中x≥1且x≠2).
(其中x≥1且x≠2).
(1)求函数 的反函数
的反函数 ;
;
(2)设 ,求函数
,求函数 最小值及相应的x值;
最小值及相应的x值;
(3)若不等式 对于区间
对于区间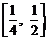 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.
21.(本题满分12分)
设 使等差数列,
使等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且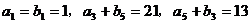 。
。
(1)求 ,
, 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 。
。
20.(本题满分12分)
设函数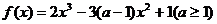
(1)求 的单调区间;
的单调区间;
(2)讨论 的极值。
的极值。
1.23=1.73,1.24=2.07,1.25=2.49,1.26=2.99)
19.(本题满分12分)
某企业为了适应市场需求,计划从2010年元月起,在每月固定投资5万元的基础上,元月份追加投资6万元,以后每月的追加投资额均为之前几个月投资额总和的20%,但每月追加部分最高限额为10万元.记第n个月的投资额为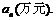
(1)求 与n的关系式;
与n的关系式;
(2)预计2010年全年共需投资多少万元?(精确到0.01,参考数据:1.22=1.44,
18.(本题满分12分)
已知函数 ;
;
(1)求函数 的最小正周期
的最小正周期
(2)令 ,判断函数
,判断函数 的奇偶性,并说明理由
的奇偶性,并说明理由
17.(本题满分10分)
已知函数
(1)求 的最大值、最小值,及取得最大、最小值时的
的最大值、最小值,及取得最大、最小值时的 的集合;
的集合;
(2)求 的单调递增区间。
的单调递增区间。
16.设正数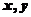 满足
满足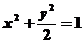 ,则
,则 最大值为
;
最大值为
;
15.15.已知定义在R上的函数 满足条件
满足条件 ,且函数
,且函数 是奇函数,给出以下四个命题:
是奇函数,给出以下四个命题:
①函数 是周期函数;
是周期函数;
②函数 的图象关于点
的图象关于点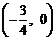 对称;
对称;
③函数 是偶函数;
是偶函数;
④函数 在R上是单调函数.
在R上是单调函数.
在上述四个命题中,真命题的序号是___________(写出所有真命题的序号)。
14.已知函数 的零点
的零点 ,且
,且 ,其中
,其中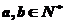 ,
,
则 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com