1．计算的结果是

　　　 A．　　　　　　　　　　　 B．　　　　　　　　　　 C． 　　　　　　　　　　 D．

20．解：(1)定义域为，，令，则，

当变化时，，的变化情况如下表：

	+
	↗		↘

∴的单调增区间为；单调减区间为.　　　　　　　　　　

(2)由(1)知在上单调递增，在上单调递减，所以，

当时，即时，在上单调递增，∴

当时， 在上单调递减，∴　　　　

当时，即时，在上单调递增，在上单调递减，

∴下面比较的大小，　　　　

∵　

∴若，则此时

若，则此时 　

综上得：

当时，；

当时，，　　　　　　　　　　　　　 ………………12分

19.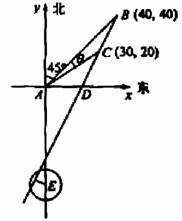解　 (I)如图，AB=40，AC=10，

由于,所以cos=

由余弦定理得BC=

所以船的行驶速度为(海里/小时).

(2)　 如图所示，以A为原点建立平面直角坐标系，

设点B、C的坐标分别是B(x₁，y₂), C(x₁，y₂),BC与x轴的交点为D.由题设有，x₁=y₁= AB=40,x₂=ACcos,

y₂=ACsin所以过点B、C的直线l的斜率k=,直线l的方程为y=2x-40.又点E(0，-55)到直线l的距离d=

所以船会进入警戒水域.

18、解：(1)∵

∴当时，；当时，，也满足上式，

∴综上得　　　　　　　　　　　　　　　　　　　　　 ………………5分

(2)由得 ，，

数列是等比数列，其中　　　　　　　　　　　　　　　　　　 　　

　　　　　　　　　 ………………10分

(3)

∴

两式相减得：　

∴　　　　　　　　　　　　　　　　　　　 ………………15分

17．解：(1) 因为，即，

所以，

即 ，

得 .　　 所以,或(不成立).

即 , 得，所以.

又因为，则，或(舍去)

得

(2)，　

　又, 即 ，　 　　　　

得

16.解：(1)设的最小正周期为，得　

由得　

又，解得　

令，即，解得

∴　

(2)∵函数的周期为

又∴　

令，∵ ∴

如图在上有两个不同的解的充要条件是

∴方程在时恰好有两个不同的解的充要条件是，

即实数的取值范围是

15．解：(Ⅰ) 因为，故集合应分为和两种情况

(1)时，

(2)时，　

所以得,故实数的取值范围为　　　

(Ⅱ)由得，解得

若真假，则

若假真，则

故实数的取值范围为或　　

11、　　　 12、　　　　 13、6　　　　　 14、.

6、1　　　　　 7、7　　　　 8、14　　　　　　 9、　　　　　 10、②④

1、3　　 2、　　　　 3、　　　　　 4、　　　　　 5、－8