2．f(x) = -2x+1

　　　 1 从左至右图象上升还是下降 ______?

　　　 2 在区间 ____________ 上，随着x的增

大，f(x)的值随着 ________ ．

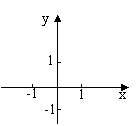
1．f(x) = x

　　　 1 从左至右图象上升还是下降 ______?

　　　 2 在区间 ____________ 上，随着x的增

大，f(x)的值随着 ________ ．

2．　 画出下列函数的图象，观察其变化规律：

1．　 观察下列各个函数的图象，并说说它们分别反映了相应函数的哪些变化规律：

1 随x的增大，y的值有什么变化？

2 能否看出函数的最大、最小值？

3 函数图象是否具有某种对称性？

课本P₂₈ 习题1．2(A组) 第8-12题 (B组)第2、3题

理解函数的三种表示方法，在具体的实际问题中能够选用恰当的表示法来表示函数，注意分段函数的表示方法及其图象的画法．

(一)典型例题

例1．某种笔记本的单价是5元，买x (x∈{1，2，3，4，5})个笔记本需要y元．试用三种表示法表示函数y=f(x) ．

分析：注意本例的设问，此处“y=f(x)”有三种含义，它可以是解析表达式，可以是图象，也可以是对应值表．

解：(略)

注意：

1 函数图象既可以是连续的曲线，也可以是直线、折线、离散的点等等，注意判断一个图形是否是函数图象的依据；

2 解析法：必须注明函数的定义域；

3 图象法：是否连线；

4 列表法：选取的自变量要有代表性，应能反映定义域的特征．

巩固练习：

课本P₂₇练习第1题

例2．下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级及班级平均分表：

请你对这三们同学在高一学年度的数学学习情况做一个分析．

分析：本例应引导学生分析题目要求，做学情分析，具体要分析什么？怎么分析？借助什么工具？

解：(略)

注意：

1 本例为了研究学生的学习情况，将离散的点用虚线连接，这样更便于研究成绩的变化特点；

2 本例能否用解析法？为什么？

巩固练习：

课本P₂₇练习第2题

例3．画出函数y = | x | ．

解：(略)

巩固练习：课本P₂₇练习第3题

拓展练习：

任意画一个函数y=f(x)的图象，然后作出y=|f(x)| 和 y=f (|x|) 的图象，并尝试简要说明三者(图象)之间的关系．

课本P₂₇练习第3题

例4．某市郊空调公共汽车的票价按下列规则制定：

(1) 乘坐汽车5公里以内，票价2元；

(2) 5公里以上，每增加5公里，票价增加1元(不足5公里按5公里计算)．

已知两个相邻的公共汽车站间相距约为1公里，如果沿途(包括起点站和终点站)设20个汽车站，请根据题意，写出票价与里程之间的函数解析式，并画出函数的图象．

分析：本例是一个实际问题，有具体的实际意义．根据实际情况公共汽车到站才能停车，所以行车里程只能取整数值．

解：设票价为y元，里程为x公里，同根据题意，

如果某空调汽车运行路线中设20个汽车站(包括起点站和终点站)，那么汽车行驶的里程约为19公里，所以自变量x的取值范围是{x∈N^*| x≤19}．

由空调汽车票价制定的规定，可得到以下函数解析式：

　 　()

根据这个函数解析式，可画出函数图象，如下图所示：

注意：

1 本例具有实际背景，所以解题时应考虑其实际意义；

2 本题可否用列表法表示函数，如果可以，应怎样列表？

实践与拓展：

请你设计一张乘车价目表，让售票员和乘客非常容易地知道任意两站之间的票价．(可以实地考查一下某公交车线路)

说明：象上面两例中的函数，称为分段函数．

注意：分段函数的解析式不能写成几个不同的方程，而就写函数值几种不同的表达式并用一个左大括号括起来，并分别注明各部分的自变量的取值情况．

2.　　　　 常用的函数表示法及各自的优点：

(1)解析法；

(2)图象法；

(3)列表法．

1.　　　　 复习：函数的概念；

补充习题