
第一节:单项选择(共20小题,每小题0.5分,满分10分)
1. - Good-bye ! I’m going back to my hometown this afternoon.
-________
|
A. Have a nice trip. |
B. Congratulations! |
|
C. Take your time. |
D. I couldn’t agree more. |
22.(本小题满分14分)
已知数列 的前n项和
的前n项和 满足:
满足: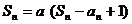 (
( 为常数,且
为常数,且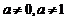 ).
).
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设 ,若数列
,若数列 为等比数列,求
为等比数列,求 的值;
的值;
(Ⅲ)在满足条件(Ⅱ)的情形下,设
 ,数列
,数列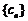 的前n项和为
的前n项和为 ,
,
求证: .
.
21.(本小题满分14分)
设椭圆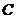 :
: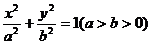 的左、右焦点分别为
的左、右焦点分别为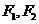 ,上顶点为
,上顶点为 ,过点
,过点 与
与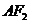 垂直的直线交
垂直的直线交 轴负半轴于点
轴负半轴于点 ,且
,且 .
.
(Ⅰ)求椭圆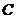 的离心率;
的离心率;
(Ⅱ)若过 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线 :
: 相切,求椭圆
相切,求椭圆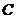 的方程;
的方程;
 (III)在(Ⅱ)的条件下,过右焦点
(III)在(Ⅱ)的条件下,过右焦点 作斜率为
作斜率为 的直线
的直线 与椭圆
与椭圆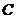 交于
交于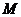 、
、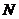 两点,在
两点,在 轴上是否存在点
轴上是否存在点 使得以
使得以 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.
20.(本小题满分12分)
设函数 ,
, ,其中
,其中 .
.
(Ⅰ)若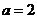 ,求曲线
,求曲线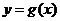 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)是否存在负数 ,使
,使 对一切正数
对一切正数 都成立?若存在,求出
都成立?若存在,求出 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
19.(本小题满分12分)
如图,在六面体 中,平面
中,平面 ∥平面
∥平面 ,
, ⊥平面
⊥平面 ,
, ,
, ,
, ∥
∥ .且
.且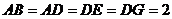 ,
, .
.
 (Ⅰ)求证:
(Ⅰ)求证: 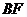 ∥平面
∥平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)
求五面体 的体积.
的体积.
18.(本小题满分12分)
某射击游戏规定:每位选手最多射击3次;射击过程中若击中目标,方可进行下一次射击,否则停止射击;同时规定第
 次射击时击中目标得
次射击时击中目标得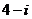 分,否则该次射击得
分,否则该次射击得 分。已知选手甲每次射击击中目标的概率为
分。已知选手甲每次射击击中目标的概率为 ,且其各次射击结果互不影响.
,且其各次射击结果互不影响.
(Ⅰ)求甲恰好射击两次的概率;
(Ⅱ)设该选手甲停止射击时的得分总和为 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
17.(本小题满分12分)
在△ABC中,设内角A、B、C的对边分别为a、b、c,
(Ⅰ)求角C的大小;
(Ⅱ)若 且
且 ,求
,求 的面积.
的面积.
16.由0,1,2,…,9这十个数字组成的、无重复数字的四位数中,个位数字与百位数字之差的绝对值等于8的个数为 个.
15.在 中,
中, ,
, ,
, 为
为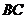 边上的点,且
边上的点,且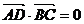 ,若
,若 ,则
,则 .
.
14.某几何体的三视图,其中正视图是腰长为 的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是
.
的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com