
22. 过抛物线
过抛物线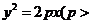

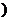 的对称轴上的定点
的对称轴上的定点 ,作直线
,作直线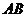 与抛物线相交于
与抛物线相交于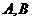 两点.
两点.
(Ⅰ)试证明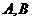 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(Ⅱ )若点
)若点 是定直线
是定直线 上的任意一点,分别记直线
上的任意一点,分别记直线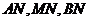 的斜率为
的斜率为 ,试探求
,试探求 之间的关系,并给出证明.
之间的关系,并给出证明.

 浙江六校联考
浙江六校联考
21. 已知函数 ,且其导函数
,且其导函数 的图像过原点.
的图像过原点.
(Ⅰ)若存在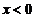 ,使得
,使得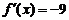 ,求
,求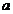 的最大值;
的最大值;
(Ⅱ) 当 时,求函数
时,求函数 的零点个数.
的零点个数.
20. 设数列 的前
的前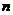 项和为
项和为 ,点
,点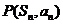 在直线
在直线 上,
上, 为常数,
为常数, .
.
(Ⅰ)求 ;
;
(Ⅱ)若数列 的公比
的公比 ,数列
,数列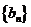 满足
满足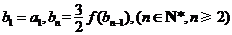 ,求证:
,求证: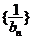 为等差
为等差 数列,并求
数列,并求 ;
;
(III)设数列 满足
满足 ,
,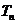 为数列
为数列 的前
的前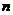 项和,且存在实数
项和,且存在实数 满足
满足 ,
,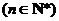 ,求
,求 的最大值.
的最大值.
19. 如图,在直角梯形
如图,在直角梯形 中,
中, ,
,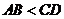 ,
, 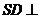 平面
平面 ,
, ,
,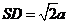 .
.
(Ⅰ)求证:平面 平面
平面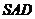 ;
;
(Ⅱ)设 的中点为
的中点为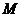 ,当
,当 为何值时,能使
为何值时,能使 ? 请给出证明.
? 请给出证明.
18.已知向量
(Ⅰ)求 .
.
(Ⅱ)若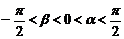 ,且
,且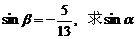 的值.
的值.
17.定义在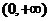 上函数
上函数 满足
满足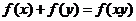 ,且当
,且当 时,
时,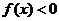 ,若不等式
,若不等式 对任意
对任意 恒成立,则实数
恒成立,则实数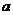 的取值范围是
▲ .
的取值范围是
▲ .
16. 已知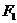 、
、 分别为椭圆
分别为椭圆 的左、右焦点,P为椭圆上一点
的左、右焦点,P为椭圆上一点 ,Q是
,Q是 轴上的一个动点,若
轴上的一个动点,若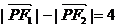 ,则
,则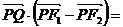 ___▲______ .
___▲______ .
15. 已知关于x的一次函数 .设集合
.设集合 和
和 ,分别从集合
,分别从集合 和
和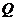 中随机取一个数作为
中随机取一个数作为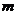 和
和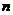 ,则函数
,则函数 是减函数的概率____▲ .
是减函数的概率____▲ .
14. 在三角形ABC中,A=1200,AB=5,BC=7,则 的值为 ▲ .
的值为 ▲ .
13. 若非负实数 满足
满足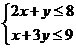 ,则
,则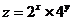 的最大值为 ▲ .
的最大值为 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com