
7. 设NA代表阿伏加德罗常数,下列说法中正确的是
A.60 g二氧化硅与12 g金刚石中含有的共价键数均为4NA
B.氧气与臭氧的混合气体含NA个氧原子时,其体积在标准状况下为11.2 L
C.4 g重水(D2O)中所含中子数为2NA
D.含0.1 mol FeCl3的溶液中阳离子个数为0.1NA
6. 对于工农业生产和日常生活中与化学有关的问题,下列认识正确的是
A.明矾净水与液氯净水的原理相同
B.冬季形成的大雾属于气溶胶
C.镀层破损后,镀铜铁板比镀锌铁板更耐腐蚀
D.太阳能电池要用到高纯硅,其中硅的作用是把化学能转变为电能
5.下面是某人在摄食后及运动过程中血糖平衡的调节示意图。其相关叙述中正确的是
 A.摄食后1小时内,分泌物甲增多主要是促进血糖合成糖元
A.摄食后1小时内,分泌物甲增多主要是促进血糖合成糖元
B.分泌物乙中主要含有胰岛B细胞和肾上腺分泌的两种激素
C.2-2.5小时分泌物乙增多,它能促进肝糖元的分解和脂肪大量转化成葡萄糖
D.从图中可看出,血糖浓度的相对稳定是分泌物甲和分泌物乙协同作用的结果
4.下面是某同学绘制的正常人体内部分物质代谢过程示意图。相关说法中错误的是
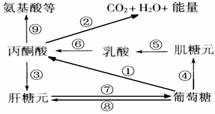 A.完成图中①⑤过程的场所是细胞质基质,完成②过程的场所是线粒体
A.完成图中①⑤过程的场所是细胞质基质,完成②过程的场所是线粒体
B.人在较长时间剧烈运动时,主要通过④⑤过程产生ATP直接供能
C.图中⑨过程所示的转氨基作用所形成的氨基酸,不可能是必需氨基酸
D.糖尿病患者体内的①④⑧⑨过程都不能正常完成
3. 食虫植物猪笼草的分泌液能将昆虫消化作为自己的养料来源。下列有关验证猪笼草分泌液中含有蛋白酶的实验设计方案中,正确的是
A.实验组和对照组加入猪笼草的分泌液,再分别加入等量的双缩脲试剂和清水
B.实验组和对照组分别加入等量的猪笼草的分泌液和清水,再加入双缩脲试剂
C.实验结果是加入双缩脲试剂后实验组紫色反应逐渐消失,对照组无颜色变化
D.实验原理是酶具有专一性的特点和双缩脲试剂与蛋白质作用可产生紫色反应
2. 将某植物幼苗培养在适宜浓度的完全营养液中,如图所示。下列相关叙述中正确的是
 A.3天后测定发现Ca2+浓度未变,说明植物吸收水和Ca2+的过程相同
A.3天后测定发现Ca2+浓度未变,说明植物吸收水和Ca2+的过程相同
B.该植物的叶片在衰老脱落前后,叶片中氮的含量无明显降低
C.培养一段时间后,该植物幼苗生长越来越差,甚至会萎蔫死亡
D.若该植物是大豆,则能将空气中的N2通过生物固氮形成NH3
1. 在下列实验装置①号试管中加入14C氨基酸一段时间后,按图示方法步骤进行处理。其相关叙述中,错误的是
在下列实验装置①号试管中加入14C氨基酸一段时间后,按图示方法步骤进行处理。其相关叙述中,错误的是
A.鸡的红细胞在蒸馏水中也会发生渗透作用吸水,最终可导致细胞破裂
B.14C氨基酸进入鸡的红细胞内的方式与小麦根尖表皮细胞吸收K+的方式相同
|
D.除去细菌或蓝藻的细胞壁后按上图同样的方法步骤处理,结果得不到核糖体
22.解:(1)∵ 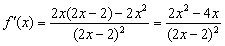 ,
,
∴ 由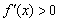 有x<0或x>2,由
有x<0或x>2,由 有0<x<2且x≠1,
有0<x<2且x≠1,
即f (x)的单调递增区间为(-∞,0),(2,+∞),单调递减区间为(0,1),(1,2).
………………………………………………………………………………………4分
(2)由题有 ,整理得2Sn=an(1-an), ①
,整理得2Sn=an(1-an), ①
∴ 当n=1时,2S1=a1(1-a1),解得a1=-1,或a1=0(舍).
当n≥2时,2Sn-1=an-1(1-an-1), ②
于是①-②得2an=an- -an-1+
-an-1+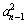 ,
,
整理得an+an-1=(an-1-an)(an-1+an),
由已知有an+an-1≠0,
∴ an-an-1=-1(常数).
∴ {an}是以-1为首项,-1为公差的等差数列.
∴ an=-n.………………………………………………………………………9分
(3)∵ an=-n,
∴ 原不等式即为 ,等价于
,等价于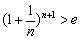 .
.
两边同取对数得 ,
,
即证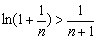 .
.
构造函数 ,
,
∵ 
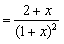 ,
,
显然当x≥0时, ,
,
∴ g(x)在 上是增函数.
上是增函数.
∴  ,即
,即 ,整理即得
,整理即得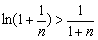 .
.
故原不等式得证.………………………………………………………………14分
21.解:(1)设-e≤x<0,则0<-x≤e,
∴ f (-x)=a(-x)+ln(-x),
已知f (x)是奇函数可得f (-x)=-f (x).
∴ -f (x)=-ax+ln(-x),即f (x)=ax-ln(-x).
∴ f (x)= ………………………………………………4分
………………………………………………4分
(2)x∈ 时,
时,
令 ,得
,得 .…………………………………………………………5分
.…………………………………………………………5分
①当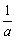 ≤-e,即-
≤-e,即- ≤a<0时,
≤a<0时,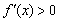 .
.
故f (x)在 上是增函数.
上是增函数.
∴ f (x)min=f (-e)=-ae-1=3,
解得 (舍).………………………………………………………8分
(舍).………………………………………………………8分
②当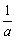 >-e,即
>-e,即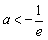 时,则
时,则
|
x |
[-e,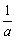 ) ) |
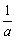 |
(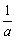 ,0) ,0) |
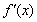 |
- |
0 |
+ |
 |
↘ |
最小值 |
↗ |
∴ f (x)min= =
= =3,解得
=3,解得 .
.
综上所述,存在实数a=-e2满足条件.………………………………………12分
20.解:(1)令y=f (x)=ax+2-1,于是y+1=ax+2,
∴ x+2=loga(y+1),即x=loga(y+1)-2,
∴ 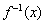 =loga(x+1)-2(x>-1).………………………………………………3分
=loga(x+1)-2(x>-1).………………………………………………3分
(2)当0<a<1时,
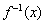 max=loga(0+1)-2=-2,
max=loga(0+1)-2=-2,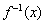 min=loga(1+1)-2=loga2-2,
min=loga(1+1)-2=loga2-2,
∴ -2-(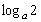 -2)=2,解得
-2)=2,解得 或
或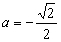 (舍).
(舍).
当a>1时,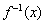 max=loga2-2,
max=loga2-2,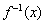 min=-2,
min=-2,
∴  ,解得
,解得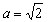 或
或 (舍).
(舍).
∴ 综上所述, 或
或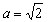 .……………………………………………7分
.……………………………………………7分
(3)由已知有loga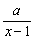 ≤loga(x+1)-2,
≤loga(x+1)-2,
即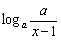 ≤
≤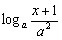 对任意的
对任意的 恒成立.
恒成立.
∵  ,
,
∴ 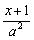 ≤
≤ .①
.①
由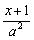 >0且
>0且 >0知x+1>0且x-1>0,即x>1,
>0知x+1>0且x-1>0,即x>1,
于是①式可变形为x2-1≤a3,
即等价于不等式x2≤a3+1对任意的 恒成立.
恒成立.
∵ u=a3+1在 上是增函数,
上是增函数,
∴  ≤a3+1≤
≤a3+1≤ ,于是x2≤
,于是x2≤ ,
,
解得 ≤x≤
≤x≤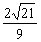 .
.
结合x>1得1<x≤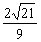 .
.
∴ 满足条件的x的取值范围为 .…………………………………12分
.…………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com