
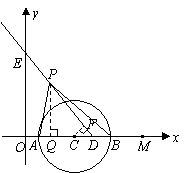
030]如图,已知射线DE与 轴和
轴和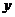 轴分别交于点
轴分别交于点 和点
和点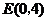 .动点
.动点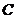 从点
从点 出发,以1个单位长度/秒的速度沿
出发,以1个单位长度/秒的速度沿 轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为
轴向左作匀速运动,与此同时,动点P从点D出发,也以1个单位长度/秒的速度沿射线DE的方向作匀速运动.设运动时间为 秒.
秒.
(1)请用含 的代数式分别表示出点C与点P的坐标;
的代数式分别表示出点C与点P的坐标;
(2)以点C为圆心、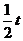 个单位长度为半径的
个单位长度为半径的 与
与 轴交于A、B两点(点A在点B的左侧),连接PA、PB.
轴交于A、B两点(点A在点B的左侧),连接PA、PB.
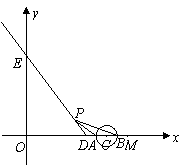 ①当
①当 与射线DE有公共点时,求
与射线DE有公共点时,求 的取值范围;
的取值范围;
②当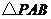 为等腰三角形时,求
为等腰三角形时,求 的值.
的值.
029]已知二次函数 。
。
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点。
(2)设a<0,当此函数图象与x轴的两个交点的距离为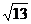 时,求出此二次函数的解析式。
时,求出此二次函数的解析式。
(3)若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为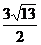 ,若存在求出P点坐标,若不存在请说明理由。
,若存在求出P点坐标,若不存在请说明理由。
030]解:(1)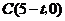 ,
, .····················································· (2分)
.····················································· (2分)
(2)①当 的圆心
的圆心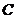 由点
由点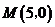 向左运动,使点
向左运动,使点 到点
到点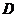 并随
并随 继续向左运动时,
继续向左运动时,
有 ,即
,即 .
.
当点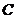 在点
在点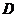 左侧时,过点
左侧时,过点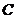 作
作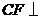 射线
射线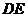 ,垂足为
,垂足为 ,则由
,则由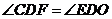 ,
,
得 ,则
,则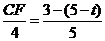 .解得
.解得 .
.
由
 ,即
,即 ,解得
,解得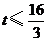 .
.
 当
当 与射线
与射线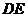 有公共点时,
有公共点时, 的取值范围为
的取值范围为 .··························· (5分)
.··························· (5分)
②当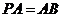 时,过
时,过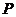 作
作 轴,垂足为
轴,垂足为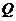 ,有
,有
 .
.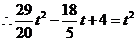 ,即
,即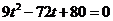 .
.
 解得
解得 .····································· (7分)
.····································· (7分)
当 时,有
时,有 ,
,
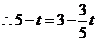 .解得
.解得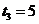 .·························· (9分)
.·························· (9分)
当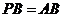 时,有
时,有
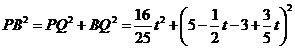 .
.
 ,即
,即 .
.
解得 (不合题意,舍去).························································· (11分)
(不合题意,舍去).························································· (11分)
 当
当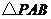 是等腰三角形时,
是等腰三角形时, ,或
,或 ,或
,或 ,或
,或 .··············· (12分)
.··············· (12分)
029]解(1)因为△=
所以不论a为何实数,此函数图象与x轴总有两个交点。…………(2分)
(2)设x1、x2是 的两个根,则
的两个根,则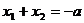 ,
, ,因两交点的距离是
,因两交点的距离是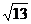 ,所以
,所以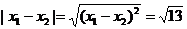 。…………(4分)
。…………(4分)
即:
变形为: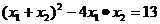 ……………………………………(5分)
……………………………………(5分)
所以: ,整理得:
,整理得: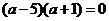
解方程得: ,又因为:a<0,所以:a=-1
,又因为:a<0,所以:a=-1
所以:此二次函数的解析式为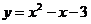 …………………………(6分)
…………………………(6分)
(3)设点P的坐标为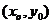 ,因为函数图象与x轴的两个交点间的距离等于
,因为函数图象与x轴的两个交点间的距离等于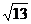 ,所以:AB=
,所以:AB=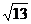 ,所以:S△PAB=
,所以:S△PAB=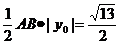
所以: 即:
即: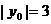 ,则
,则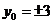
当 时,
时,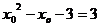 ,即
,即
解此方程得: =-2或3,当
=-2或3,当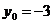 时,
时,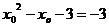 ,即
,即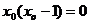
解此方程得: =0或1
=0或1
综上所述,所以存在这样的P点,P点坐标是(-2,3), (3,3), (0, -3)或(1, -3)。…(12分)
028]解:(1)(5′) ∵抛物线与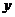 轴交于点(0,3),
轴交于点(0,3),
 ∴设抛物线解析式为
∴设抛物线解析式为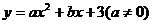 (1′)
(1′)
根据题意,得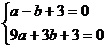 ,解得
,解得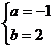
∴抛物线的解析式为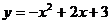 (5′)
(5′)
(2)(5′)由顶点坐标公式得顶点坐标为(1,4) (2′)
设对称轴与x轴的交点为F
∴四边形ABDE的面积=
=
=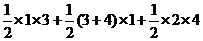 =9 (5′)
=9 (5′)
(3)(2′)相似
如图,BD= ;∴BE=
;∴BE=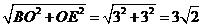
DE= ∴
∴ ,
, 
即:
 ,所以
,所以 是直角三角形
是直角三角形
∴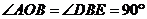 ,且
,且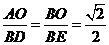 ,
,
∴ ∽
∽ (2′)
(2′)
027]解:(1)设抛物线的解析式为: , 把A(3,0)代入解析式求得
, 把A(3,0)代入解析式求得
所以 ,设直线AB的解析式为:
,设直线AB的解析式为: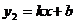
由 求得B点的坐标为
求得B点的坐标为 把
把 ,
,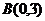 代入
代入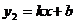 中
中
解得: 所以
所以 6分
6分
(2)因为C点坐标为(1,4) ,所以当x=1时,y1=4,y2=2所以CD=4-2=2 8分
 (平方单位)
(平方单位)
(3)假设存在符合条件的点P,设P点的横坐标为x,△PAB的铅垂高为h,
则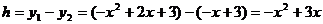 ,由S△PAB=
,由S△PAB=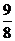 S△CAB
S△CAB
得: ,化简得:
,化简得: 解得,
解得,
将 代入
代入 中,解得P点坐标为
中,解得P点坐标为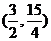
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com