21．(本题满分12分)已知f (x)是定义在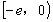∪上的奇函数，当x∈时，f (x)=ax+lnx，其中a<0，a∈R，e为自然对数的底数．

　　 (1)求f (x)的解析式；

　　 (2)是否存在实数a，使得当x∈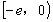时，f (x)的最小值为3？如果存在，求出实数a的值；如果不存在，请说明理由．

20．(本题满分12分)已知函数f (x)=a^x+2-1(a>0，且a≠1)的反函数为．

(1)求；

(2)若在[0，1]上的最大值比最小值大2，求a的值；

(3)设函数，求不等式g(x)≤对任意的恒成立的x的取值范围．

19．(本题满分12分)等差数列{a_n}的各项均为正数，a₁=3，前n项和为S_n，数列{b_n}为等比数列，b₁=1，且b₂S₂=4，b₃S₃=．

(1)求a_n与b_n；

(2)记数列{}的前n项和为T_n，且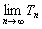=T，求使b_n≥成立的所有正整数n．

18．(本题满分12分)国庆前夕，我国具有自主知识产权的“人甲型H1N1流感病毒核酸检测试剂盒”(简称试剂盒)在上海进行批量生产，这种“试剂盒”不仅成本低操作简单，而且可以准确诊断出“甲流感”病情，为甲型H1N1流感疫情的防控再添一道安全屏障．某医院在得到“试剂盒”的第一时间，特别选择了知道诊断结论的5位发热病人(其中“甲流感”患者只占少数)，对病情做了一次验证性检测．已知如果任意抽检2人，恰有1位是“甲流感”患者的概率为．

(1)求出这5位发热病人中“甲流感”患者的人数；

(2)若用“试剂盒”逐个检测这5位发热病人，直到能确定“甲流感”患者为止，设ξ表示检测次数，求ξ的分布列及数学期望Eξ．

17．(本题满分12分)已知函数的定义域为集合A，不等式≥1的解集为B．

(1)求(_RA)∩B；

(2)记A∪B=C，若集合M={x∈R||x-a|<4}满足M∩C=Æ，求实数a的取值范围．

16．已知二次函数f (x)=x²-mx+m(x∈R)同时满足：(1)不等式f (x)≤0的解集有且只有一个元素；(2)在定义域内存在0<x₁<x₂，使得不等式f (x₁)>f (x₂)成立．设数列{a_n}的前n项和S_n=f (n)，．我们把所有满足b_i ·b_i+1＜0的正整数i的个数叫做数列{b_n}的异号数．根据以上信息，给出下列五个命题：

①m=0；

②m=4；

③数列{a_n}的通项公式为a_n=2n-5；

④数列{b_n}的异号数为2；

⑤数列{b_n}的异号数为3．

其中正确命题的序号为　　　　　　 ．(写出所有正确命题的序号)

15．曲线y=xsinx+cosx在x=π处的切线与函数y=e^ax(a∈R，a≠0)的图象在x=0处的切线平行，则实数a=　　　　　 ．

14．为庆祝祖国母亲60华诞，教育局举行“我的祖国”歌咏比赛，某中学师生踊跃报名参加．据统计，报名的学生和教师的人数之比为5∶1，学校决定按分层抽样的方法从报名的师生中抽取60人组队参加比赛．已知教师甲被抽到的概率为，则报名的学生人数是　　　　　 ．

13．在等差数列{a_n}中，如果a_n=a_n+2，那么公差d=　　　　　 ．

12．已知g(x)是定义在[-1，1]上的奇函数，且在区间[0，1]上满足三个条件：①对于任意的x₁，x₂∈[0，1]，当x₁<x₂时，恒有g(x₁)≤g(x₂)成立，②，③g(x)+g(1-x)=1．则

A．　　　　　　　 B．　　　　　　　 C．　　　　　　　 D．

第Ⅱ卷 (非选择题　 共90分)

答第Ⅱ卷前，考生务必将自己的姓名、准考证号用钢笔或圆珠笔(蓝、黑色)写在答题卷密封线内相应的位置．答案写在答题卷上，不能答在试题卷上．