
21.(本小题14分)
已知数列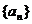 的前n项和为
的前n项和为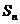 ,对一切正整数n,点
,对一切正整数n,点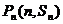 都在函数
都在函数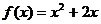 的图像上,且在点
的图像上,且在点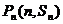 处的切线的斜率为
处的切线的斜率为
(I)求数列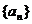 的通项公式;
的通项公式;
(II)若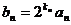 ,求数列
,求数列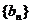 的前n项和
的前n项和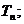
(III)设 等差数列
等差数列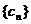 的任一项
的任一项 ,其中c1是
,其中c1是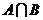 的最小数,
的最小数, 求数列
求数列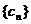 的通项公式.
的通项公式.
20.(本小题12分)
已知椭圆 的左、右焦点分别为F1、F2,其中F2也是抛物线
的左、右焦点分别为F1、F2,其中F2也是抛物线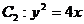 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且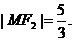
(I)求椭圆C1的方程;
(II)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B、D在直线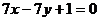 上,求直线AC的方程.
上,求直线AC的方程.
19.(本小题12分)
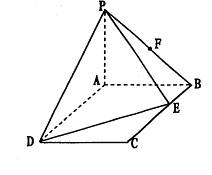
如图,PA⊥ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在 边BC上移动.
(I)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(II)证明:无论点E在边BC的何处,都有PE⊥AF;
(III)当BE等于何值时,二面角P-DE-A的大小为45°.
18.(本小题12分)
为预防“甲型H1N1流感”的扩散,某两个大国的研究所A、B均对其进行了研究.若独立地研究“甲型H1N1流感”疫苗,研究成功的概率分别为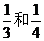 ;若资源共享,则提高了效率,即他们研究成功的概率比独立地研究时至少有一个研制成功的概率提高了50%.又疫苗研制成功获得经济效益a万元,而资源共享时所得的经济效益只能两个研究所平均分配.请你给A研究所参谋:是否应该采取与B研究所合作的方式来研究疫苗,并说明理由.
;若资源共享,则提高了效率,即他们研究成功的概率比独立地研究时至少有一个研制成功的概率提高了50%.又疫苗研制成功获得经济效益a万元,而资源共享时所得的经济效益只能两个研究所平均分配.请你给A研究所参谋:是否应该采取与B研究所合作的方式来研究疫苗,并说明理由.
17.(本小题12分)
A、B是直线 图像的两个相邻交点,且
图像的两个相邻交点,且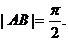
(I)求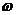 的值;
的值;
(II)在锐角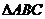 中,a,b,c分别是角A,B,C的对边,若
中,a,b,c分别是角A,B,C的对边,若 的面积为
的面积为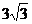 ,求a的值.
,求a的值.
16.给出下列四个命题:
①已知 点
点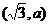 到直线
到直线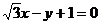 的距离为1;
的距离为1;
②若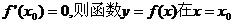 取得极值;
取得极值;
③ ,则函数
,则函数 的值域为R;
的值域为R;
④在极坐标系中,点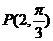 到直线
到直线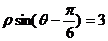 的距离是2.
的距离是2.
其中真命题是 (把你认为正确的命题序号都填在横线上)
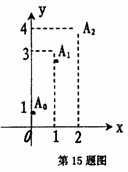
15.已知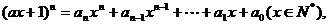
点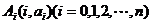 部分图象如图所示,则实数a的值为 .
部分图象如图所示,则实数a的值为 .
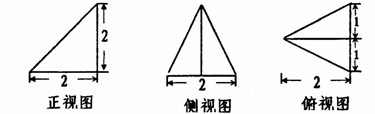
14.已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),则这个几何体的体积是 cm3.
13.甲、乙等五名志愿者被分配到上海世博会中国馆、英国馆、澳大利亚馆、俄罗斯馆四个不同的岗位服务,每个岗位至少一名志愿者,则甲、乙两人各自独立承担一个岗位工作的分法共有 种(用数字做答)
12.已知抛物线 焦点F恰好是双曲线
焦点F恰好是双曲线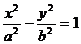 的右焦点,且双曲线过点
的右焦点,且双曲线过点 则该双曲线的渐近线方程为
.
则该双曲线的渐近线方程为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com