
例1.设椭圆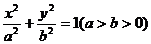 的左焦点为
的左焦点为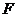 ,上顶点为
,上顶点为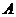 ,过点
,过点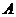 与
与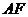 垂直的直线分别交椭圆和
垂直的直线分别交椭圆和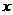 轴正半轴于
轴正半轴于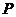 ,
,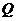 两点,且
两点,且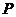 分向量
分向量 所成的比为8∶5.
所成的比为8∶5.
(1)求椭圆的离心率;
(2)若过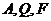 三点的圆恰好与直线
三点的圆恰好与直线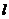 :
: 相切,求椭圆方程.
相切,求椭圆方程.
例2. 设双曲线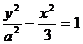 的两个焦点分别为
的两个焦点分别为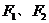 ,离心率为2。
,离心率为2。
(I)若A、B分别为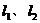 上的点,且
上的点,且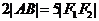 ,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
(II)过点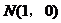 能否作出直线
能否作出直线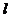 ,使
,使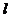 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且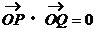 。若存在,求出直线
。若存在,求出直线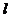 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
例3.过抛物线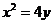 上不同两点A、B分别作抛物线的切线相交于P点,
上不同两点A、B分别作抛物线的切线相交于P点,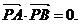
(1)求点P的轨迹方程;
(2)已知点F(0,1),是否存在实数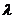 使得
使得 ?若存在,求出
?若存在,求出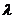 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
5.已知双曲线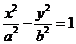
 的半焦距是
的半焦距是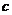 ,直线
,直线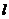 过点
过点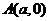 ,
,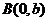 ,若原点到直线
,若原点到直线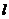 的距离为
的距离为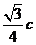 ,则双曲线的离心率为 ____________
,则双曲线的离心率为 ____________
4.已知(4,2)是直线l被椭圆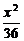 +
+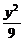 =1所截得的线段的中点,则l的方程是____________.
=1所截得的线段的中点,则l的方程是____________.
2.双曲线x2-y2=1的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是( )
A.(-∞,0)B.(1,+∞) C.(-∞,0)∪(1,+∞)D.(-∞,-1)∪(1,+∞)
3过抛物线y2=4x焦点的直线交抛物线于A、B两点,已知|AB|=8,O为坐标原点,则 △OAB的重心的横坐标为____________.
1.过点(2,4)作直线与抛物线y2=8x只有一个公共点,这样的直线有
A.1条 B.2条 C.3条 D.4条
4.直线与圆锥曲线的关系体现了解析几何的基本思想方法,即数形结合思想。解决这类问题,一方面要解题思路正确,方法选择得当;另一方面在数、式、方程的变形时,应注意简化,如要善于运用韦达定理,充分利用图形的几何性质等等。选择恰当参数对深入研究直线与圆锥曲线的关系非常重要,解题的同时要注意运用“整体思想”,减少运算量。
3.直线与圆锥曲线相交成弦的问题。包括弦长的计算,弦的中点,最值,由弦长或弦的中点的几何性质确定直线方程或圆锥曲线的方程,对称性问题等等。解决这些问题经常转化为它们所对应的方程构成的方程组是否有解或解的个数问题。对相交弦问题及中点问题要正确运用“设而不求”。涉及焦点弦的问题还可以利用圆锥曲线的焦半径公式。
2.
1.
44.(总分10分) 学生得分:
(1)自然原因:
(2分)
人为原因:
(2分)
(2)
4分
(3) (2分)
“华安、连城、永安、漳平一中,龙海二中,泉港一中”六校联考
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com