
17. 解:
解:




16.解: (Ⅰ)因为 ,所以
,所以 得
得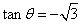 又
又 ,所以
,所以 =
=
(Ⅱ)因为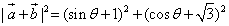 =
=
所以当 =
= 时,
时,  的最大值为5+4=9
故
的最大值为5+4=9
故 的最大值为3
的最大值为3
9. 10.
10.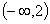 11.
11.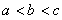 12.
12. 13.(-∞,-2]∪[-1,3) 14.2 15.0;1
13.(-∞,-2]∪[-1,3) 14.2 15.0;1
CACB CBBD
21.(本小题满分13分)已知函数f (x) = x + 2
(1)判断函数f (x)在区间(0, +∞)上的单调性,并加以证明;
(2)如果关于x的方程f (x) = kx2有四个不同的实数解,求实数k的取值范围.
20.(本小题满分13分)已知二次函数 满足
满足 ,且关于
,且关于 的方程
的方程 的两实数根分别在区间(-3,-2),(0,1)内。
的两实数根分别在区间(-3,-2),(0,1)内。
(1)求实数 的取值范围;
的取值范围;
(2)若函数 在区间(-1-
在区间(-1- ,1-
,1- )上具有单调性,求实数
)上具有单调性,求实数 的取值范围
的取值范围
19. (本小题满分13分)今年我市的一个农贸公司计划收购某种农产品,如果按去年各季度该农产品市场价的最佳近似值m收购,并按每100元纳税10元(又称征税率为10个百分点),计划可收购a万担 政府为了鼓励收购公司收购这种农产品,决定征收税率降低x个百分点,预测收购量可增加2个百分点
(1) 经计算农贸公司的收购价为m=200(元/担),写出降低征税率后,税收y(万元)与x的函数关系式;;
(2) 要使此项税收值在税率调节后,不少于原计划收购的税收值的83 2%,试确定x的取值范围
18.(本小题满分12分)设函数 是定义在
是定义在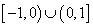 上的奇函数,当
上的奇函数,当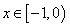 时,
时,
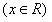
(1) 当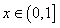 时,求
时,求 的解析式;
的解析式;
(2) 若 ,试判断
,试判断 在
在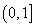 上的单调性,并证明你的结论
上的单调性,并证明你的结论
17.(本小题满分12分)已知 =
= ,求
,求 的值.
的值.
16.(本小题满分12分)已知向量 ,
, ,
, .
.
(Ⅰ)若 ,求
,求 ; (Ⅱ)求
; (Ⅱ)求 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com