
3.试题类型:选择题12道,填空题4道,简答题5道。
2.考察范围:基本初等函数及性质
21. (本小题满分14分)已知函数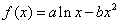 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若方程 在
在 内有两个不等实根,求
内有两个不等实根,求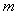 的取值范围(其中
的取值范围(其中 为自然对数的底数,
为自然对数的底数, );
);
(Ⅲ)令 ,如果
,如果 图象与
图象与 轴交于
轴交于 ,
,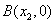 (
( ),
), 中点为
中点为 ,求证:
,求证: 在
在 处的导数
处的导数 .
.
2010届“三校联考”统一考试(文科)数学试题
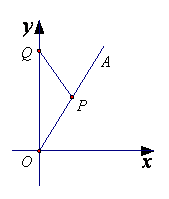
20. (本小题满分14分)如图所示,在直角坐标系 中,射线
中,射线 在第一象限,且与
在第一象限,且与 轴的正半轴成定角
轴的正半轴成定角 ,动点
,动点 在射线
在射线 上运动,动点
上运动,动点 在
在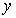 轴的正半轴上运动,
轴的正半轴上运动, 的面积为
的面积为 .
.
(Ⅰ)求线段 中点
中点 的轨迹
的轨迹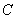 的方程;
的方程;
(Ⅱ) 是曲线
是曲线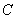 上的动点,
上的动点,  到
到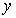 轴的距离之和为
轴的距离之和为 ,设
,设 为
为 到
到 轴的距离之积.问:是否存在最大的常数
轴的距离之积.问:是否存在最大的常数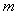 ,使
,使 恒成立?若存在,求出这个
恒成立?若存在,求出这个 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
19. (本小题满分14分)某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮;现按同样的规律刺绣(小正方形的摆放规律相同),设第
(本小题满分14分)某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮;现按同样的规律刺绣(小正方形的摆放规律相同),设第 个图形包含
个图形包含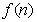 个小正方形.
个小正方形.
(Ⅰ)求出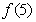 的值;
的值;
(Ⅱ)利用合情推理的“归纳推理思想”,归纳出 与
与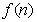 之间的关系式,并根据你得到的关系式求出
之间的关系式,并根据你得到的关系式求出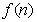 的表达式;
的表达式;
(Ⅲ)求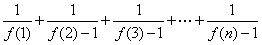 的值.
的值.
18. (本小题满分14分)一个多面体的直观图,正(主)视图,侧(左)视图如下所示,其中正(主)视图、侧(左)视图为边长为 的正方形。
的正方形。
(Ⅰ)请在指定的框内画出多面体的俯视图;
(Ⅱ)若多面体底面对角线 交于点
交于点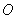 ,
,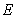 为线段
为线段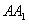 的中点,求证:
的中点,求证:  平面
平面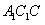
(Ⅲ)求该多面体的表面积;
17. (本小题满分12分)某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(Ⅰ)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
 (Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
(Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
 |
5 |
0.050 |
|
第2组 |
 |
① |
0.350 |
|
第3组 |
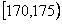 |
30 |
② |
|
第4组 |
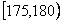 |
20 |
0.200 |
|
第5组 |
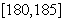 |
10 |
0.100 |
|
合计 |
100 |
1.00 |

16. (本小题满分12分)已知函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)已知 ,且
,且 ,求
,求 的值.
的值.
(二)选做题(14、15题考生只能从中选作一题, 如果两题都做,按第一题得分给分)
14. (坐标系与参数方程选做题)在极坐标系中,直线
(坐标系与参数方程选做题)在极坐标系中,直线 的方程为
的方程为 , 则点
, 则点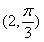 到直线
到直线 的距离为
_________ .
的距离为
_________ .
15. (几何证明选讲选做题)如图,  为⊙O的直径,弦
为⊙O的直径,弦 于点
于点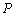 ,
,
 ,
, ,则
,则 的值为 __________.
的值为 __________.
2010届“三校联考”统一考试(文科)数学答题卷
第Ⅱ卷
二。填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
11. 12. 13.
14. 15.
(一)必做题(11~13题)
11.已知椭圆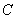 的中心在坐标原点,椭圆的两个焦点分别为
的中心在坐标原点,椭圆的两个焦点分别为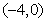 和
和 ,
,
且经过点 ,则该椭圆的方程为___________________
,则该椭圆的方程为___________________
12.设 满足条件
满足条件 ,则点
,则点 构成的平面区域面积为________.
构成的平面区域面积为________.
13. 设定义在 上的函数
上的函数 ,若关于
,若关于 的方程
的方程
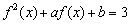 有且只有3个不同实数解
有且只有3个不同实数解 、
、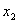 、
、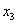 ,且
,且 ,则
,则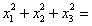 ______
______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com