
15.(2007福建)在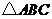 中,
中, ,
, .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若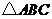 最大边的边长为
最大边的边长为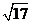 ,求最小边的边长.
,求最小边的边长.
解 (Ⅰ) ,
,
 .又
.又 ,
, .
.
(Ⅱ) ,
, 边最大,即
边最大,即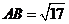 .
.
又∵tanA<tanB,A、B
 角
角 最小,
最小, 边为最小边.
边为最小边.
由 且
且 ,
,
得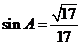 .由
.由 得:BC=AB·
得:BC=AB·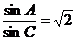 .
.
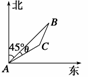
14.(2007宁夏,海南)如图,测量河对岸的塔高 时,
时,
可以选与塔底 在同一水平面内
在同一水平面内
的两个侧点 与
与 .现测得
.现测得 ,
,
并在点 测得塔顶
测得塔顶 的仰角为
的仰角为 ,求塔高
,求塔高 .
.
解 在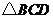 中,
中, .
.
由正弦定理得 .
.
所以 .
.
在Rt△ABC中, .
.
14.(2008湖南)在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东 且与点A相距40
且与点A相距40 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东 +
+ (其中sin
(其中sin =
= ,
,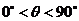 )且与点A相距10
)且与点A相距10 海里的位置C.
海里的位置C.
 (I)求该船的行驶速度(单位:海里/小时);
(I)求该船的行驶速度(单位:海里/小时);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
解 (I)如图,AB=40 ,AC=10
,AC=10 ,
,
由于 ,所以cos
,所以cos =
=
 由余弦定理得BC=
由余弦定理得BC=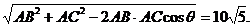
所以船的行驶速度为 (海里/小时).
(海里/小时).
(II)解法一 如图所示,以A为原点建立平面直角坐
标系,
设点B、C的坐标分别是B(x1,y2), C(x1,y2),
BC与x轴的交点为D.
由题设有,x1=y1=  AB=40,
AB=40,
x2=ACcos ,
,
y2=ACsin
所以过点B、C的直线l的斜率k=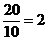 ,直线l的方程为y=2x-40.
,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=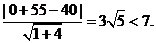
 所以船会进入警戒水域.
所以船会进入警戒水域.
解法二 如图所示,设直线AE与BC的延长线相交于点Q.
在△ABC中,由余弦定理得,

= =
= .
.
从而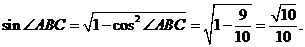
在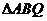 中,由正弦定理得,
中,由正弦定理得,
AQ=
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.
过点E作EP BC于点P,则EP为点E到直线BC的距离.
BC于点P,则EP为点E到直线BC的距离.
在Rt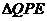 中,PE=QE·sin
中,PE=QE·sin
 =
=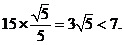
所以船会进入警戒水域.
12.(2007重庆)在△ABC中,AB=1,BC=2,B=60°,则AC= .
答案 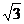
11.(2007湖南)在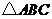 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若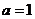 ,b=
,b= ,
, ,则
,则 .
.
答案 
10.(2007北京)在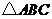 中,若
中,若 ,
,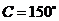 ,
, ,则
,则 .
.
答案

9.(2008湖北)在△ 中,三个角
中,三个角 的对边边长分别为
的对边边长分别为 ,则
,则
 的值为
.
的值为
.
答案 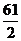
8.(2008浙江)在△ABC中,角A、B、C所对的边分别为 、b、c ,若
、b、c ,若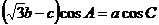 ,则
,则 _________.
_________.
答案 
7.(2005福建)在△ABC中,∠A=90°, 的值是
.
的值是
.
答案 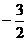
6. (2006年全卷I) 的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,
(2006年全卷I) 的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,
且c=2a,则cosB= ( )
A. B.
B. C.
C. D.
D.
答案 B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com