
2. (陕西省西安铁一中2009届高三12月月考)如图,边长为2的等
边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=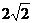 ,
,
M为BC的中点
(Ⅰ)证明:AM⊥PM ;
(Ⅱ)求二面角P-AM-D的大小;
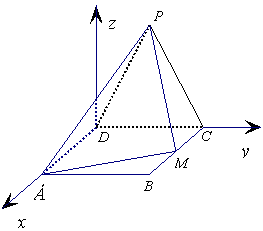 (Ⅲ)求点D到平面AMP的距离。
(Ⅲ)求点D到平面AMP的距离。
(Ⅰ) 证明 以D点为原点,分别以直线DA、DC为x轴、y轴,
建立如图所示的空间直角坐标系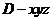 ,
,
依题意,可得

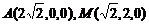
∴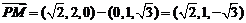
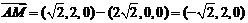
∴
即 ,∴AM⊥PM .
,∴AM⊥PM .
(Ⅱ)解 设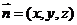 ,且
,且 平面PAM,则
平面PAM,则
 即
即
∴ ,
, 
取 ,得
,得
取 ,显然
,显然 平面ABCD, ∴
平面ABCD, ∴
结合图形可知,二面角P-AM-D为45°;
(Ⅲ) 设点D到平面PAM的距离为 ,由(Ⅱ)可知
,由(Ⅱ)可知 与平面PAM垂直,则
与平面PAM垂直,则
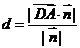 =
=
即点D到平面PAM的距离为
2009年联考题
解答题
1.

 (湖南省衡阳市八中2009届高三第三次月考试题)如图,P-ABCD是正四棱锥,
(湖南省衡阳市八中2009届高三第三次月考试题)如图,P-ABCD是正四棱锥, 是正方体,其中
是正方体,其中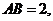

(1)求证: ;
;
(2)求平面PAD与平面 所成的锐二面角
所成的锐二面角 的余弦值;
的余弦值;
(3)求 到平面PAD的距离
到平面PAD的距离
以 为
为 轴,
轴,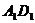 为
为 轴,
轴, 为
为 轴建立空间直角坐标系
轴建立空间直角坐标系
(1)证明 设E是BD的中点,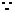 P-ABCD是正四棱锥,∴
P-ABCD是正四棱锥,∴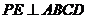
又 , ∴
, ∴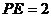 ∴
∴ ∴
∴ 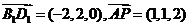
∴  , 即
, 即 。
。
(2)解 设平面PAD的法向量是 ,
,

∴ 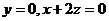 取
取 得
得 ,又平面
,又平面 的法向量是
的法向量是 ∴
∴ 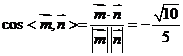 , ∴
, ∴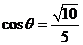 。
。
 (3)解
(3)解 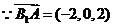 ∴
∴ 到平面PAD的距离
到平面PAD的距离 。
。
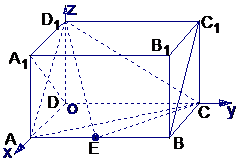
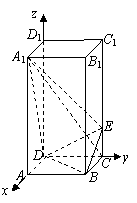
7. (2005江西)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(2005江西)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为 .
.
以D为坐标原点,直线DA,DC,DD1分别为x, y, z轴,建 立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),
E(1,x,0),A(1,0,0),C(0,2,0)
(1)证明 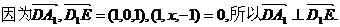
(2)解 因为E为AB的中点,则E(1,1,0),
 从而
从而 ,
,
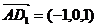 ,
,
设平面ACD1的法向量为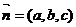 ,
,
则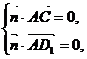
也即 ,得
,得 ,从而
,从而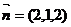 ,所以点E到平面AD1C的距离为
,所以点E到平面AD1C的距离为

(3)解 设平面D1EC的法向量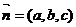 ,
,
∴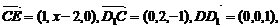
由 令b=1, ∴c=2,a=2-x,
令b=1, ∴c=2,a=2-x,
∴
依题意
∴ (不合,舍去),
(不合,舍去), .
.
∴AE=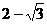 时,二面角D1-EC-D的大小为
时,二面角D1-EC-D的大小为 .
.
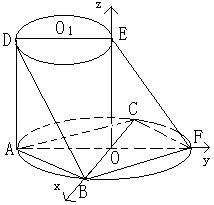
6. (2006广东卷)如图所示,AF、DE分别是⊙O、⊙O1的直
(2006广东卷)如图所示,AF、DE分别是⊙O、⊙O1的直
径.AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,
AB=AC=6,OE//AD.
(Ⅰ)求二面角B-AD-F的大小;
(Ⅱ)求直线BD与EF所成的角.
解 (Ⅰ)∵AD与两圆所在的平面均垂直,
∴AD⊥AB, AD⊥AF,故∠BAD是二面角B-AD-F的平面角,
依题意可知,ABCD是正方形,所以∠BAD=450.
即二面角B-AD-F的大小为450.
(Ⅱ)以O为原点,BC、AF、OE所在直线为坐标轴,建立空间直角坐标系(如图所示),则O(0,0,0),A(0, ,0),B(
,0),B( ,0,0),D(0,
,0,0),D(0, ,8),E(0,0,8),F(0,
,8),E(0,0,8),F(0, ,0)
,0)
 所以,
所以,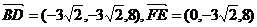
 .
.
设异面直线BD与EF所成角为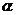 ,
,
则
直线BD与EF所成的角为
5. (2007福建理•18)如图,正三棱柱ABC-A1B1C1的所有
(2007福建理•18)如图,正三棱柱ABC-A1B1C1的所有
棱长都为2,D为CC1中点。
(Ⅰ)求证:AB1⊥面A1BD;
(Ⅱ)求二面角A-A1D-B的大小;
(Ⅲ)求点C到平面A1BD的距离;
(Ⅰ)证明 取 中点
中点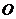 ,连结
,连结 .
.
 为正三角形,
为正三角形, .
.
 在正三棱柱
在正三棱柱 中,平面
中,平面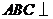 平面
平面 ,
,
 平面
平面 .
.
取 中点
中点 ,以
,以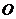 为原点,
为原点, ,
,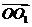 ,
, 的方向为
的方向为 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则 ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, .
.
 ,
, ,
,

 ,
,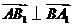 .
.
 平面
平面 .
.
(Ⅱ)解 设平面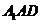 的法向量为
的法向量为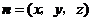 .
.
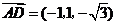 ,
, .
.
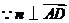 ,
, ,
,



令 得
得 为平面
为平面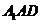 的一个法向量.
的一个法向量.
由(Ⅰ)知 平面
平面 ,
,
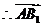 为平面
为平面 的法向量.
的法向量.
 ,
, .
.
 二面角
二面角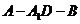 的大小为
的大小为 .
.
(Ⅲ)解 由(Ⅱ), 为平面
为平面 法向量,
法向量,
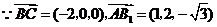 .
.
 点
点 到平面
到平面 的距离
的距离 .
.
4.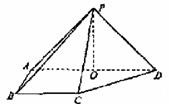 (2008福建18)如图,在四棱锥P-ABCD中,则面PAD⊥底面 ABCD,侧棱PA=PD=
(2008福建18)如图,在四棱锥P-ABCD中,则面PAD⊥底面 ABCD,侧棱PA=PD= ,底面ABCD为直角梯形,
,底面ABCD为直角梯形,
其中BC∥ AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PD与CD所成角的大小;
(Ⅲ)线段AD上是否存在点Q,使得它到平面PCD的距离为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅰ)证明 在△PAD中PA=PD,O为AD中点,所以PO⊥AD,
又侧面PAD⊥底面ABCD,平面 平面ABCD=AD,
平面ABCD=AD,
 平面PAD,
平面PAD,
所以PO⊥平面ABCD.
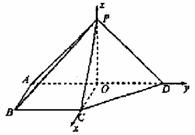 (Ⅱ)解 以O为坐标原点,
(Ⅱ)解 以O为坐标原点, 的方向分别为x轴、y轴、
的方向分别为x轴、y轴、
z轴的正方向,建立空间直角坐标系O-xyz,依题意,易得
A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),P(0,0,1),
所以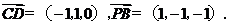
所以异面直线PB与CD所成的角是arccos ,
,
(Ⅲ)解 假设存在点Q,使得它到平面PCD的距离为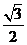 ,
,
由(Ⅱ)知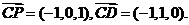
设平面PCD的法向量为n=(x0,y0,z0).
则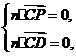 所以
所以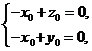 即
即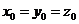 ,
,
取x0=1,得平面PCD的一个法向量为n=(1,1,1).
设 由
由 ,得
,得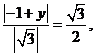
解y=- 或y=
或y= (舍去),
(舍去),
此时 ,所以存在点Q满足题意,此时
,所以存在点Q满足题意,此时 .
.
3. (2008湖南17 )如图所示,四棱锥P-ABCD的底面
ABCD是边长为1的菱形,∠BCD=60°,E是CD
的中点,PA⊥底面ABCD,PA=2.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的大小.
如图所示,以A为原点,建立空间直角坐标系.则相关各点的
坐标分别是A(0,0,0),B(1,0,0),


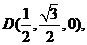 P(0,0,2),
P(0,0,2),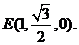
(Ⅰ)证明 因为 ,
,
平面PAB的一个法向量是 ,
,
所以 共线.从而BE⊥平面PAB.
共线.从而BE⊥平面PAB.
又因为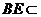 平面PBE,
平面PBE,
故平面PBE⊥平面PAB.
(Ⅱ)解 易知

设 是平面PBE的一个法向量,则由
是平面PBE的一个法向量,则由 得
得
 所以
所以
设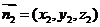 是平面PAD的一个法向量,则由
是平面PAD的一个法向量,则由 得
得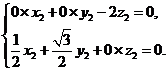 所以
所以 故可取
故可取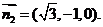
于是,
故平面PAD和平面PBE所成二面角(锐角)的大小是
2. (2008安徽)如图,在四棱锥 中,底面
中,底面 四边长
四边长
 为1的菱形,
为1的菱形,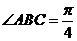 ,
,  ,
, 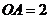 ,
,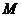 为
为
 的中点,
的中点, 为
为 的中点
的中点
(Ⅰ)证明:直线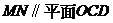
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
作 于点P,如图,分别以AB,AP,AO所在直线为
于点P,如图,分别以AB,AP,AO所在直线为
 轴建立坐标系
轴建立坐标系
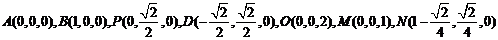 ,
,
(1)证明 
设平面OCD的法向量为 ,则
,则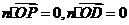
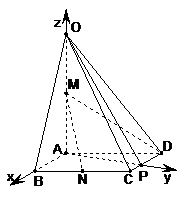 即
即 
取 ,解得
,解得
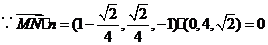
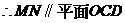
(2)解 设 与
与 所成的角为
所成的角为 ,
,
 ,
,  与
与 所成角的大小为
所成角的大小为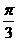 .
.
(3)解 设点B到平面OCD的距离为 ,
,
则 为
为 在向量
在向量 上的投影的绝对值,
上的投影的绝对值,
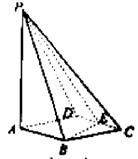 由
由 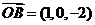 , 得
, 得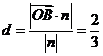 .所以点B到平面OCD的距离为
.所以点B到平面OCD的距离为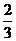
2009年高考题
2005-2008年高考题
解答题
1.  (2008全国Ⅱ19)(本小题满分12分)
(2008全国Ⅱ19)(本小题满分12分)
如图,正四棱柱 中,
中, ,点
,点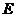 在
在 上且
上且 .
.
(Ⅰ)证明: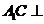 平面
平面 ;
;
(Ⅱ)求二面角 的大小.
的大小.
以 为坐标原点,射线
为坐标原点,射线 为
为 轴的正半轴,
轴的正半轴,
 建立如图所示直角坐标系
建立如图所示直角坐标系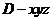 .依题设,
.依题设,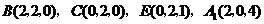 .
.
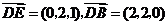 ,
,
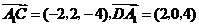 .
.
(Ⅰ)证明 因为 ,
, ,
,
故 ,
, .
.
又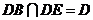 ,
,
所以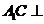 平面
平面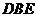 .
.
(Ⅱ)解 设向量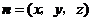 是平面
是平面 的法向量,则
的法向量,则
 ,
,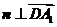 .
.
故 ,
, .
.
令 ,则
,则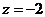 ,
, ,
, .
.
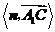 等于二面角
等于二面角 的平面角,
的平面角,
 .
.
所以二面角 的大小为
的大小为 .
.
14.(本题满分14分)
 如图,在直三棱柱
如图,在直三棱柱 中,
中, ,
,
 ,求二面角
,求二面角 的大小。
的大小。 

简答: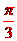
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com