
9、(2007年辽宁)已知数列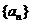 ,
, 与函数
与函数 ,
, ,
, 满足条件:
满足条件:
 ,
, .
.
(I)若 ,
, ,
,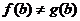 ,
, 存在,求
存在,求 的取值范围;
的取值范围;
(II)若函数 为
为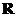 上的增函数,
上的增函数, ,
, ,
,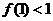 ,证明对任意
,证明对任意 ,
, (用
(用 表示).
表示).
(Ⅰ)解法一:由题设知 得
得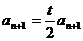 ,又已知
,又已知 ,可得
,可得

由
 其首项为
其首项为 .于是
.于是

又liman存在,可得0<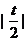 <1,所以-2<t<2且
<1,所以-2<t<2且
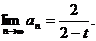
解法二.由题设知tbn+1=2bn+1,且 可得
可得

由 可知
可知 ,所以
,所以 是首项为
是首项为 ,公
,公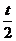 的等比数列.
的等比数列.

由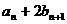 可知,若
可知,若 存在,则
存在,则 存在.于是可得0<
存在.于是可得0<
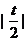 <1,所以-1<t
<1,所以-1<t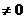 .
.
 =2
=2

解法三:由题设知tbn+1=2bn+1,即
 ①
①
于是有
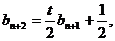 ②
②
②-①得

由 ,所以
,所以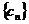 是首项为b公比为
是首项为b公比为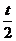 的等比数列,于是
的等比数列,于是
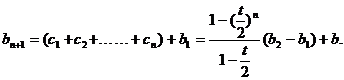
 (b2-b1)+2b.
(b2-b1)+2b.
又 存在,可得0<
存在,可得0<
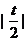 <1,所以-2<t<2且
<1,所以-2<t<2且

说明:数列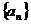 通项公式的求法和结果的表达形式均不唯一,其他过程和结果参照以标准.
通项公式的求法和结果的表达形式均不唯一,其他过程和结果参照以标准.
(Ⅱ)证明:因为 .
.
下面用数学归纳法证明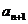 <
< .
.
(1)当n=1时,由f(x)为增函数,且 <1,得
<1,得
 <1
<1
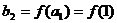 <1
<1
 <
< ,
,
即 <
< ,结论成立.
,结论成立.
(2)假设n=k时结论成立,即 <
< .由f(x)为增函数,得
.由f(x)为增函数,得
 <f
<f 即
即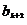 <
< 进而得
进而得
 <f(
<f( )即
)即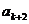 <
< .
.
这就是说当n=k+1时,结论也成立.
根据(1)和(2)可知,对任意的 ,
,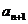 <
<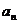 .
.
8、(2005年上海2) .
.
答案 0
7、(2006天津)设函数 ,点
,点 表示坐标原点,点
表示坐标原点,点 ,若向量
,若向量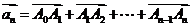 ,
,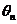 是
是 与
与 的夹角,(其中
的夹角,(其中 ),设
),设
 ,则
,则 =
.
=
.
[解析]函数 ,点
,点 表示坐标原点,点
表示坐标原点,点 ,若向量
,若向量
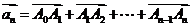 =
=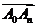 ,
,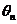 是
是 与
与 的夹角,
的夹角, (其
(其
中 ),设
),设
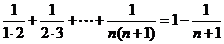 ,则
,则 =1.
=1.
答案 1
6、(2007年全国Ⅱ理16)已知数列的通项an=-5n+2,其前n项和为Sn, 则 = .
= .
答案 -
[解析]数列的通项an=-5n+2,其前n项和为Sn ,则
,则 =-
=- .
.
5、(2008上海2)计算: .
.
答案 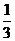
4、(2005年全国Ⅱ理5)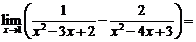 ( )
( )
A 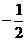 B
B
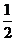 C
C
 D
D

[解析] 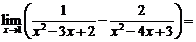

 ,选(A)
,选(A)
答案 A
3、(2006湖南)数列{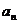 }满足:
}满足: ,且对于任意的正整数m,n都有
,且对于任意的正整数m,n都有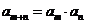 ,则
,则
 ( )
( )
A.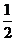 B.
B.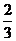 C.
C. D.2
D.2
[解析]数列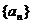 满足:
满足: 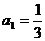 , 且对任意正整数
, 且对任意正整数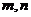 都有
都有
 ,
,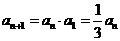 ,∴数列
,∴数列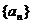 是首项为
是首项为 ,公比为
,公比为 的等比数列。
的等比数列。
 ,选A.
,选A.
答案 A
2、(2007年湖北)已知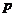 和
和 是两个不相等的正整数,且
是两个不相等的正整数,且 ,则
,则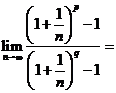 ( )
( )
A.0 B.1 C. D.
D.
答案 C
1、(2007年江西) ( )
( )
A.等于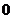 B.等于
B.等于 C.等于
C.等于 D.不存在
D.不存在
答案 B
3、(09陕西理13)设等差数列 的前n项和为
的前n项和为 ,若
,若 ,则
,则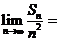 .
.
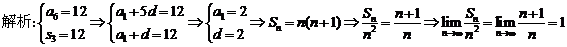 答案 1
答案 1
2005-2008年高考题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com