
3、(2009上海奉贤区模拟考)在1,2,3,4,5这五个数字中任取不重复的3个数字组成一个三位数,则组成的三位数是奇数的概率是
。(用分数表示)答案 
2、(2009上海八校联考)已知集合 ,
, ,(
,( 可以等于
可以等于 ),从集合
),从集合 中任取一元素,则该元素的模为
中任取一元素,则该元素的模为 的概率为______________。
的概率为______________。
答案 
1、(2009上海十四校联考)在集合 中任取一个元素,所取元素
中任取一个元素,所取元素
恰好满足方程 的概率是
的概率是
答案

14、(湖北省八校2009届高三第二次联考文)在某社区举办的《2008奥运知识有奖问答比赛》中,甲、乙、丙三人同时回答一道有关奥运知识的问题,已知甲回答对这道题的概率是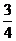 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是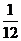 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 .
.
(Ⅰ)求乙、丙两人各自回答对这道题的概率.
(Ⅱ)求甲、乙、丙三人中恰有两人回答对该题的概率.
 解:
解: 记“甲回答对这道题”、“ 乙回答对这道题”、“丙回答对这道题”分别为事件
记“甲回答对这道题”、“ 乙回答对这道题”、“丙回答对这道题”分别为事件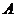 、
、 、
、 ,则
,则 ,且有
,且有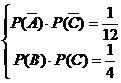 ,即
,即
∴
(2)由(1) ,
,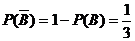 .
.
则甲、乙、丙三人中恰有两人回答对该题的概率为:
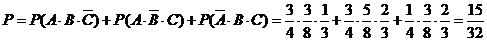
15(09江西高二其中)某科技公司遇到一个技术难题,紧急成立甲、乙两个攻关小组,按
要求各自单独进行为期一个月的技术攻关,同时决定对攻关期满就攻克技术难题的小组给予奖励.已知此技术难题在攻关期满时被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为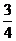 .
.
(1)设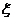 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求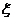 的分布列及
的分布列及 ;
;
(2)设 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递减”为事件
在定义域内单调递减”为事件 ,求事件
,求事件 的概率.
的概率.
解:记“甲攻关小组获奖”为事件A,则 ,记“乙攻关小组获奖”为事件B,则
,记“乙攻关小组获奖”为事件B,则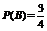 .
.
(1)由题意,ξ的所有可能取值为0,1,2.
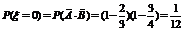 ,
,

 ,
,
∴ξ的分布列为:
|
ξ |
0 |
1 |
2 |
|
P |
 |
 |
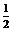 |
∴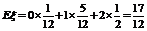 .
.
(2)∵获奖攻关小组数的可能取值为0,1,2,相对应没有获奖的攻关小组的取值为2,1,0.∴η的可能取值为0,4.
当η=0时, 在定义域内是增函数.
在定义域内是增函数.
当η=4时, 在定义域内是减函数.
在定义域内是减函数.
∴ .
.
9月份更新
13、(2009龙岩一中文)将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为5的概率;
(2)两数中至少有一个奇数的概率;
(3)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率.
解: 将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件
(1)记“两数之和为5”为事件A,则事件A中含有4个基本事件,
所以P(A)= ;
;
答:两数之和为5的概率为 .
.
(2)记“两数中至少有一个奇数”为事件B,则事件B与“两数均为偶数”为对立事件,
所以P(B)= ;
;
答:两数中至少有一个奇数的概率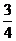 .
.
(3)基本事件总数为36,点(x,y)在圆x2+y2=15的内部记为事件C,则C包含8个事件,
所以P(C)= .
.
答:点(x,y)在圆x2+y2=15的内部的概率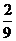 .
.
12、(北京市石景山区2009年4月高三一模理)
某工厂在试验阶段大量生产一种零件.这种零件有 、
、 两项技术
两项技术
指标需要检测,设各项技术指标达标与否互不影响.若 项技术指标达标的概率为
项技术指标达标的概率为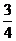 ,有且仅有一项技术指标达标的概率为
,有且仅有一项技术指标达标的概率为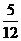 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(Ⅰ)求一个零件经过检测为合格品的概率;
(Ⅱ)任意依次抽出 个零件进行检测,求其中至多
个零件进行检测,求其中至多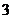 个零件是合格品的概率;
个零件是合格品的概率;
(Ⅲ)任意依次抽取该种零件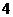 个,设
个,设 表示其中合格品的个数,求
表示其中合格品的个数,求 与
与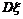 .
.
解:(Ⅰ)设 、
、 两项技术指标达标的概率分别为
两项技术指标达标的概率分别为 、
、 .
.
由题意得: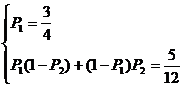 ,
,
解得: .
.
∴ 一个零件经过检测为合格品的概率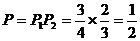 .
.
(Ⅱ)任意抽出5个零件进行检查,其中至多3个零件是合格品的概率为:
 .
.
(Ⅲ)依题意知  -
- ,
, ,
, .
.
11、(2009高三冲刺)甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个(其中“贝贝”、“晶晶”、“欢欢”、
“迎迎”和“妮妮各一个”),现以投掷一个骰子的方式进行游戏,规则如下:当出现向上
的点数是奇数时,甲赢得乙一个福娃;否则乙赢得甲一个福娃,规定掷骰子的次数达次
时,或在此前某人已赢得所有福娃时游戏终止。记游戏终止时投掷骰子的次数为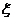
(1)求掷骰子的次数为7的概率;
(2)求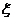 的分布列及数学期望E
的分布列及数学期望E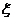 。
。
解:(1)当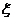 =7时,甲赢意味着“第七次甲赢,前6次赢5次,但根据规则,前5次中
=7时,甲赢意味着“第七次甲赢,前6次赢5次,但根据规则,前5次中
必输1次”,由规则,每次甲赢或乙赢的概率均为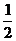 ,因此
,因此
 =
=
(2)设游戏终止时骰子向上的点数是奇数出现的次数为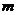 ,向上的点数是偶数出现的次
,向上的点数是偶数出现的次
数为n,则由 ,可得:当
,可得:当
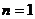 或
或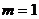 ,
, 时,
时, 当
当 ,
, 或
或 因此
因此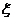 的可能取值是5、7、9
的可能取值是5、7、9
每次投掷甲赢得乙一个福娃与乙赢得甲一个福娃的可能性相同,其概率都是

所以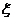 的分布列是:
的分布列是:
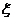 |
5 |
7 |
9 |
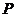 |
 |
 |
 |

10、(2009金华一中2月月考)从1,2,3,4,5,6这6个数字中, 任取2个数字相加, 其和为偶数的概率是 ______ .
答案 
9、(2009金陵中学三模)在边长为2的正三角形ABC中,以A为圆心, 为半径画一弧,分别交AB,AC于D,E.若在△ABC这一平面区域内任丢一粒豆子,则豆子落在扇形ADE内的概率是____________.
为半径画一弧,分别交AB,AC于D,E.若在△ABC这一平面区域内任丢一粒豆子,则豆子落在扇形ADE内的概率是____________.
答案 
8、 (湖北省孝感市2009届高三3月统考理)
(湖北省孝感市2009届高三3月统考理)
设三个正态分布 (
(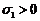 )、
)、
( )、
)、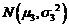 (
( )的密度函数图象
)的密度函数图象
如图所示,则 、
、 、
、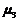 按从小到大的顺序排列
按从小到大的顺序排列
是______________; 、
、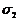 、
、 按从小到大的顺
按从小到大的顺
序排列是_____________.
答案  ,
,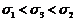
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com