
4.(2009聊城一模)设函数 。
。
(1)写出函数 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)当 时,函数
时,函数 的最大值与最小值的和为
的最大值与最小值的和为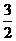 ,求
,求 的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积。
的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积。
解(1)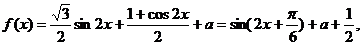 (2分)
(2分)
 (4分)
(4分)

故函数 的单调递减区间是
的单调递减区间是 。 (6分)
。 (6分)
(2)(理)
当 时,原函数的最大值与最小值的和
时,原函数的最大值与最小值的和
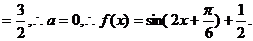 (8分)
(8分)
 的图象与x轴正半轴的第一个交点为
的图象与x轴正半轴的第一个交点为 (10分)
(10分)
所以 的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积
的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积
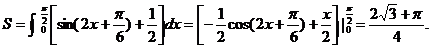 (12分)
(12分)
3.(2009日照一模)已知函数 ,给出下列四个命题:
,给出下列四个命题:
①若 ,则
,则 ; ②
; ② 的最小正周期是
的最小正周期是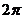 ;
;
③ 在区间
在区间 上是增函数; ④
上是增函数; ④ 的图象关于直线
的图象关于直线 对称
对称
A.①②④ B.①③ C.②③ D.③④
答案 D
2.(2009青岛一模)设函数 ,则下列结论正确的是
,则下列结论正确的是
A. 的图像关于直线
的图像关于直线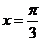 对称
对称
B. 的图像关于点
的图像关于点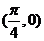 对称
对称
C.把 的图像向左平移
的图像向左平移 个单位,得到一个偶函数的图像
个单位,得到一个偶函数的图像
D. 的最小正周期为
的最小正周期为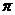 ,且在
,且在 上为增函数
上为增函数
答案 C
1.(2009滨州一模)(5)已知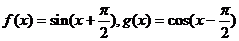 ,则
,则 的图象
的图象
A.与 的图象相同
B.与
的图象相同
B.与 的图象关于
的图象关于 轴对称
轴对称
C.向左平移 个单位,得到
个单位,得到 的图象 D.向右平移
的图象 D.向右平移 个单位,得到
个单位,得到 的图象
的图象
答案 D
24.(金华十校2009年高考模拟考试(3月)试卷)已知函数 的图象的一部分如下图所示。
的图象的一部分如下图所示。
(1)求函数 的解析式;
的解析式;
(2)当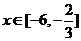 时,求函数
时,求函数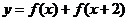 的最大值与最小值及相应的
的最大值与最小值及相应的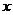 的值。
的值。

解:(1)由图像知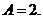
 ,
, ,
, ,又图象经过点(-1,0)
,又图象经过点(-1,0)
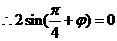
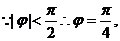

(2)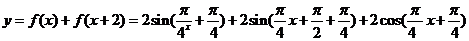

 ,
, 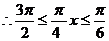
 当
当 即
即 时,
时,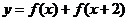 的最大值为
的最大值为 ,当
,当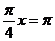 ,
,
即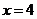 时, 最小值为
时, 最小值为
9月份更新
23.(2009届山东省实验中学高三年级第四次综合测试)已知函数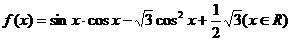 .
.
(1)求 的最小正周期;
的最小正周期;
(2)求 的单调递增区间;
的单调递增区间;
(3)求 图象的对称轴方程和对称中心的坐标.
图象的对称轴方程和对称中心的坐标.
解:
=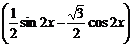 =
=
(1)T=π;
(2)由
可得单调增区间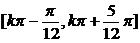 (
(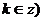 .
.
(3)由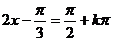 得对称轴方程为
得对称轴方程为 ,
,
由 得对称中心坐标为
得对称中心坐标为 .
.
22.(福州市普通高中2009年高中毕业班质量检查)已知 的最小正周期为
的最小正周期为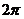 。
。
(I)求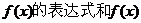 的单调递增区间;
的单调递增区间;
(II)求 的最大值和最小值
的最大值和最小值
解:(I)由已知

(II)

21.(2009玉溪一中期中) 图像的一条对称轴是直线
图像的一条对称轴是直线 。
。
(Ⅰ)求 ;
;
(Ⅱ)画出函数 在区间
在区间 上的图像。
上的图像。
解:(Ⅰ) 的图像的对称轴,
的图像的对称轴,
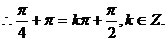

(Ⅱ)由
|
x |
0 |
 |
 |
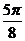 |
 |
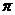 |
|
y |
 |
-1 |
0 |
1 |
0 |
 |
 故函数
故函数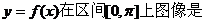
20.(2009玉溪市民族中学第四次月考)已知函数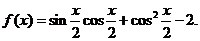
(Ⅰ)将函数 化简成
化简成 的形式,并指出
的形式,并指出 的最小正周期;
的最小正周期;
(Ⅱ)求函数 上的最大值和最小值
上的最大值和最小值
解 (Ⅰ) f(x)=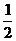 sinx+
sinx+ .
.
故f(x)的最小正周期为2π{k∈Z且k≠0}。
(Ⅱ)由π≤x≤ ,得
,得 .因为f(x)=
.因为f(x)= 在
在
[ ]上是减函数,在[
]上是减函数,在[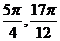 ]上是增函数,故当x=
]上是增函数,故当x= 时,f(x)有最小值-
时,f(x)有最小值-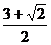 ;而f(π)=-2,f(
;而f(π)=-2,f(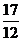 π)=-
π)=-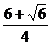 <-2,所以当x=π时,f(x)有最大值-2.
<-2,所以当x=π时,f(x)有最大值-2.
19.(山东省聊城市2009 年 高 考 模 拟 试 题)设函数 。
。
(1)写出函数 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)当 时,函数
时,函数 的最大值与最小值的和为
的最大值与最小值的和为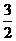 ,求a的值。
,求a的值。
解(1)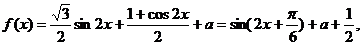


故函数 的单调递减区间是
的单调递减区间是 。
。
|

当 时,原函数的最大值与最小值的和
时,原函数的最大值与最小值的和

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com