
21.(1)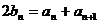 ,
, 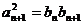 得
得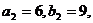
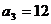 ,
,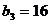 ,
,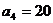 ,
,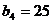 ,于是猜测
,于是猜测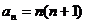 ,
,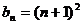 下面用数学归纳法证明
下面用数学归纳法证明
①当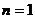 时,结论显然成立 ②假设
时,结论显然成立 ②假设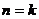 时,结论成立。即
时,结论成立。即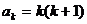 ,
, 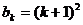 ,那么
,那么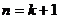 时,
时,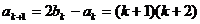 ,
,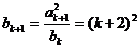 ,所以,当
,所以,当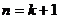 时结论成立,由(1)(2)可知
时结论成立,由(1)(2)可知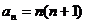 ,
,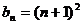 对一切正整数成立。
对一切正整数成立。
(2)证明:当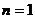 时,
时,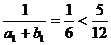 ,当
,当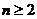 时,
时,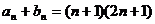
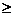
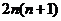 ,所以
,所以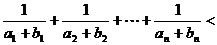
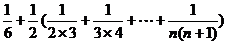
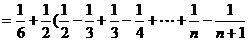 )=
)=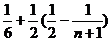
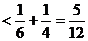 ,故原不等式成立。
,故原不等式成立。

21.(14分)在数列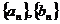 中,
中,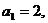
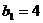 且
且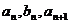 成等差数列,
成等差数列,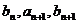 成等比数列
成等比数列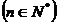 .
.
(1)求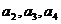 及
及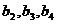 ,由此猜测
,由此猜测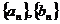 的通项公式,并用数学归纳法证明你的结论;
的通项公式,并用数学归纳法证明你的结论;
(2)证明: 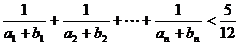
 参考答案
参考答案

增函数;在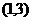 上,
上,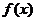 是减函数;在
是减函数;在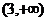 上,
上,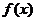 是增函数;
是增函数;
所以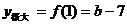 ,
,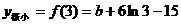
依题意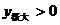 且
且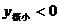 ,即
,即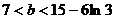
20.(14分)已知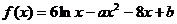
 ,且
,且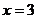 是
是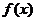 的一个极值点.
的一个极值点.
(1)求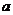 的值;
的值;
(2)若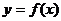 的图象与
的图象与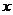 轴有且只有三个不同的交点,求
轴有且只有三个不同的交点,求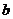 的取值范围.
的取值范围.
19. (14分)已知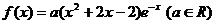 求
求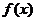 的单调区间.
的单调区间.
18.(14分)若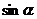 是
是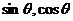 的等差中项,
的等差中项,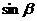 是的
是的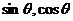 等比中项,求证:
等比中项,求证: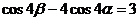
17.(14分)已知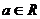 ,复数
,复数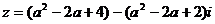 ,(
,(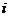 是虚数单位).
是虚数单位).
(1)判断复数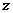 对应的点在第几象限;
对应的点在第几象限;
(2)复数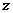 对应的点的轨迹是什么图形.
对应的点的轨迹是什么图形.
16.
 若
若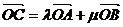 且
且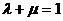 ,则
,则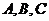 三点共线,将这一结论类比到空间,你得到的结论是
.
三点共线,将这一结论类比到空间,你得到的结论是
.
15.已知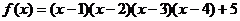 ,则
,则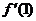 的值是
.
的值是
.
14.由曲线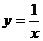 ,
,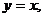
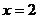 围成的平面区域的面积是_________.
围成的平面区域的面积是_________.
13.若复数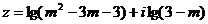 是纯虚数,则实数
是纯虚数,则实数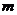 =____________.
=____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com