
21. (本题满分14分)
已知函数f(x)=x2+bsinx-2,(b∈R), F(x)=f(x)+2, 且对于任意实数x,恒有F(x-5)=F(5-x).
(1)求函数f(x)的解析式;
(2)已知函数g(x)=f(x)+2(x+1)+alnx在区间(0,1)上单调, 求实数a的取值范围;
(3)函数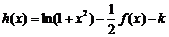 有几个零点?
有几个零点?
解:(1)由题设得:F(x)=x2+bsinx,
∵F(x-5)=F(5-x),
∴F(-x)=F(x)
∴x2-bsinx=x2+bsinx,
∴bsinx=0对于任意实数x都成立,∴b=0
∴f(x)=x2-2.
(2) 由g(x)=f(x)+2(x+1)+alnx=x2+2x+alnx,
得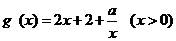 ,
,
g(x)在(0,1)上恒单调,只需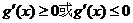 在(0,1)上恒成立.
在(0,1)上恒成立.
即 2x2+2x+a≥0或2x2+2x+a≤0在(0,1)上恒成立.
∴a≥-(2x2+2x)或a≤-(2x2+2x)在(0,1)上恒成立.
设u(x)=-(2x2+2x), x∈(0,1),易知:u(x)∈(-4,0),
∴a≥0或a≤-4.
(3) 令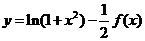 ,
,

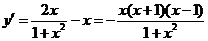 ,
,
令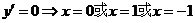 ,列表如下:
,列表如下:
|
x |
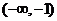 |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
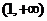 |
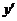 |
+ |
0 |
- |
0 |
+ |
0 |
- |
|
y |
增 |
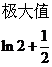 |
减 |
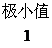 |
增 |
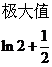 |
减 |
∴当k> 时,无零点;
时,无零点;
当k<1或k= 时,有两个零点;
时,有两个零点;
当k=1时,有三个零点;
当 时,有四个零点.
时,有四个零点.
20. (本题满分14分)已知函数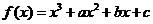 .
.
(Ⅰ)若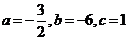 ,求
,求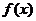 在
在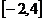 上的最大值与最小值;
上的最大值与最小值;
(Ⅱ)设函数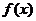 的图像关于原点
的图像关于原点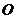 对称,在点
对称,在点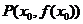 处的切线为
处的切线为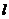 ,
,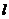 与函数
与函数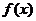 的图像交于另一点
的图像交于另一点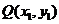 .若
.若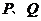 在
在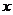 轴上的射影分别为
轴上的射影分别为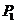 、
、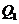 ,
,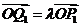 ,求
,求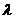 的值.
的值.
(Ⅰ)若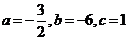 ,
,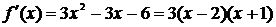
|
x |
-2 |
(-2,-1) |
-1 |
(-1,2) |
2 |
(2,4) |
4 |
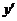 |
|
+ |
|
- |
|
+ |
|
|
y |
-1 |
增 |
 |
减 |
-9 |
增 |
17 |
最大值为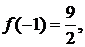 最小值为
最小值为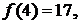

19.(本题满分13分)为应对国际金融危机对企业带来的不良影响,2009年某企业实行裁员增效,已知现有员工a人,每人每年可创纯利润1万元。据评估,在生产条件不变的条件下,每裁员1人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的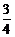 ,设该企业裁员x人后纯收益为y万元.
,设该企业裁员x人后纯收益为y万元.
(1)写出y关于x的函数关系式,并指出x的取值范围;
(2)当140<a≤280时,问企业裁员多少人,才能获得最大的经济效益?(注:在保证能获得最大经济效益的情况下,能少裁员,就尽量少裁)
解:(1)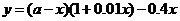
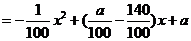
∵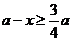 ,∴
,∴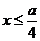 ,即x的取值范围是
,即x的取值范围是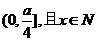 。
。
(2)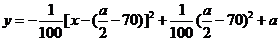 ,
,
当140<a≤280时,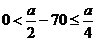 ,∴当a为偶数时,x取
,∴当a为偶数时,x取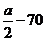 ,y取最大值;;
,y取最大值;;
当a为奇数时,x取 或
或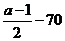 ,y取最大值.
,y取最大值.
∵尽可能少裁员,,∴x=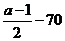 ,综上所述:当a为偶数时,应裁员
,综上所述:当a为偶数时,应裁员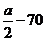 ,当a为奇数时,应裁员
,当a为奇数时,应裁员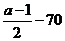 .
.
18. (本题满分13分)已知△ABC的面积S满足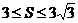 ,且
,且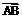 ·
·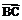 =6,
=6,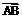 与
与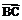 的夹角为
的夹角为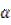 .
.
(1)求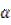 的取值范围;
的取值范围;
(2)若函数f(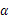 )=sin2
)=sin2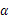 +2sin
+2sin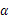 cos
cos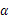 +3cos2
+3cos2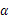 ,求f(
,求f(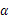 )的最小值,并指出取得最小值时的
)的最小值,并指出取得最小值时的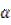 .
.
解: (1)由题意知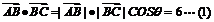
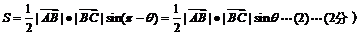
由②÷①得=tanθ即3tanθ=S……(3分)
由3≤S≤3得3≤3tanθ≤3……(4分)
又θ为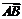 与
与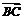 的夹角,∴θ∈(0,π)∴θ∈(,)……(6分)
的夹角,∴θ∈(0,π)∴θ∈(,)……(6分)
(2)f(θ)=sin2θ+2sinθcosθ+3cos2θ=1+sin2θ+2cos2θ
∴f(θ)=2+sin2θ+cos2θ=2+sin(2θ+)……(9分)
∵θ∈(,),∴2θ+∈(, )
∴2θ+=,即θ=时,f(θ) min= =……(13分)
17. (本题满分13分)已知函数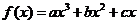 在点
在点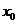 处取得极大值5,其导函数
处取得极大值5,其导函数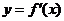 的图象经过点(1,0),(2,0),如图所示, 求:(Ⅰ)
的图象经过点(1,0),(2,0),如图所示, 求:(Ⅰ)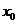 的值; (Ⅱ)a,b,c 的值.
的值; (Ⅱ)a,b,c 的值.
|
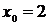
|
|
|
|
|
x |
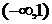 |
1 |
(1,2) |
2 |
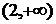 |
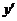 |
- |
0 |
+ |
0 |
- |
|
y |
减 |
|
增 |
|
减 |
(2)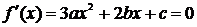 两根为1,2。
两根为1,2。
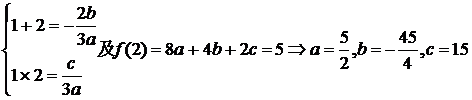
16.(13分)已知△ 顶点的直角坐标分别为
顶点的直角坐标分别为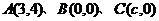 .
.
(1)若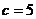 ,求sin∠
,求sin∠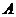 的值; (2)若∠
的值; (2)若∠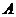 是钝角,求
是钝角,求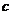 的取值范围.
的取值范围.
解 (1) 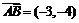 ,
, 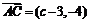 当c=5时,
当c=5时,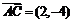
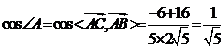 进而
进而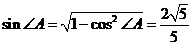
(2)若A为钝角,则AB﹒AC= -3(c-3)+( -4)2<0 解得c>
显然此时有AB和AC不共线,故当A为钝角时,c的取值范围为[ ,+
,+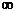 )
)
13、 6 14、 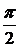 15、
15、 
11、
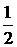 12、
12、 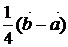
21. (本题满分14分)
已知函数f(x)=x2+bsinx-2,(b∈R), F(x)=f(x)+2, 且对于任意实数x,恒有F(x-5)=F(5-x).
(1)求函数f(x)的解析式;
(2)已知函数g(x)=f(x)+2(x+1)+alnx在区间(0,1)上单调, 求实数a的取值范围;
(3)函数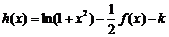 有几个零点?
有几个零点?
厦外2010届高三数学第一阶段测试卷(第Ⅱ卷)2009年10月
20. (本题满分14分)已知函数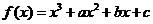 .
.
(Ⅰ)若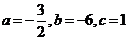 ,求
,求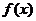 在
在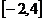 上的最大值与最小值;
上的最大值与最小值;
(Ⅱ)设函数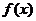 的图像关于原点
的图像关于原点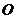 对称,在点
对称,在点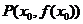 处的切线为
处的切线为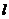 ,
,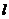 与函数
与函数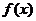 的图像交于另一点
的图像交于另一点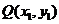 .若
.若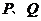 在
在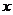 轴上的射影分别为
轴上的射影分别为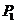 、
、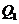 ,
,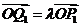 ,求
,求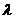 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com