

2.解方程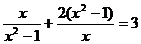 时.设
时.设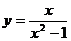 ,则原方程化为
,则原方程化为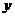 的整式方程为
的整式方程为
A.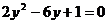 ;
B.
;
B. 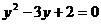 ;
;
C.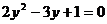 ;
D.
;
D.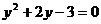 .
.
[每小题只有一个正确选项,在答题纸的相应题号的选项上用2 B铅笔填涂]
1.下列运算中,结果是 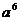 的式子是
的式子是
A. 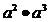 ; B.
; B. 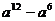 ; C.
; C. 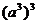 ; D.
; D. 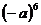 ;
;
20.(本小题满分14分)
已知函数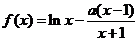 .
.
(Ⅰ) 若函数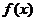 在
在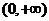 上为单调增函数,求
上为单调增函数,求 的取值范围;
的取值范围;
(Ⅱ) 设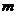 ,
,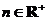 ,且
,且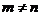 ,求证:
,求证: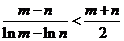 .
.
(考生务必将答案答在答题卡上,在试卷上作答无效)
北京市东城区2009-2010学年度第二学期综合练习(二)
19.(本小题满分13分)
已知数列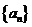 的前
的前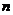 项和为
项和为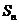 ,
,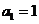 ,
,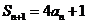 ,设
,设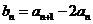 .
.
(Ⅰ)证明数列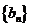 是等比数列;
是等比数列;
(Ⅱ)数列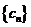 满足
满足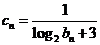
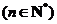 ,设
,设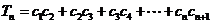 , 若对一切
, 若对一切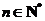 不等式
不等式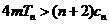 恒成立,求实数
恒成立,求实数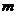 的取值范围.
的取值范围.
18.(本小题满分13分)
已知抛物线的焦点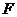 在
在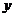 轴上,抛物线上一点
轴上,抛物线上一点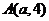 到准线的距离是
到准线的距离是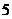 ,过点
,过点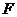 的直线与抛物线交于
的直线与抛物线交于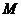 ,
,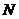 两点,过
两点,过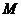 ,
,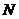 两点分别作抛物线的切线,这两条切线的交点为
两点分别作抛物线的切线,这两条切线的交点为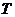 .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求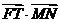 的值;
的值;
(Ⅲ)求证: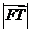 是
是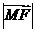 和
和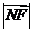 的等比中项.
的等比中项.
17.(本小题满分14分)
如图,四棱锥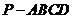 中,底面
中,底面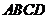 是直角梯形,
是直角梯形,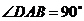 ,
,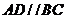 ,
,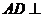 侧面
侧面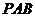 ,△
,△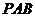 是等边三角形,
是等边三角形,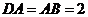 ,
, 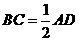 ,
,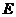 是线段
是线段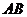 的中点.
的中点.
 (Ⅰ)求证:
(Ⅰ)求证: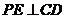 ;
;
(Ⅱ)求四棱锥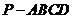 的体积;
的体积;
(Ⅲ)求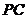 与平面
与平面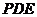 所成角的正弦值.
所成角的正弦值.
16.(本小题满分13分)
袋中装着标有数字1,2,3,4的小球各3个,从袋中任取3个小球,每个小球被取出的可能性都相等.
(Ⅰ)求取出的3个小球上的数字互不相同的概率;
(Ⅱ)用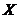 表示取出的3个小球上所标的最大数字,求随机变量
表示取出的3个小球上所标的最大数字,求随机变量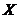 的分布列和均值.
的分布列和均值.
15. (本小题满分13分)

 在
在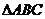 中,角
中,角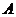 ,
,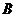 ,
,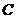 所对的边分别为
所对的边分别为 ,
,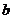 ,
,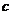 ,
, 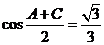 .
.
(Ⅰ)求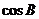 的值;
的值;
(Ⅱ)若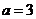 ,
,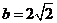 ,求
,求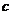 的值21.
的值21.
14. 已知数列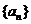 中,
中,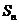 是其前
是其前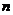 项和,若
项和,若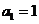 ,
,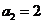 ,
,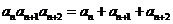 ,
,
且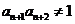 ,则
,则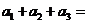 _______________,
_______________,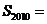 _______________.
_______________.
13. 在函数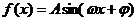
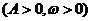 的一个周期内,当
的一个周期内,当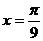 时有最大值
时有最大值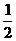 ,当
,当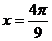 时有最小值
时有最小值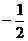 ,若
,若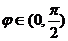 ,则函数解析式
,则函数解析式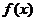 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com