

4. 配制一定物质的量浓度的NaOH溶液时,造成所配溶液的浓度偏高的是
A. 所用NaOH固体已潮解 B.定容时,俯视液面达容量瓶的刻度线
C.托盘天平的托盘上各放一张纸,调整天平平衡后,将NaOH固体放在左盘的纸上称量
D.在需用游码的托盘天平上称量NaOH固体时,砝码与固体的位置放颠倒
3. 体积相同的两个密闭的容器中分别充满O2、O3气体,当这两个容器内温度和气体密度相等时,下列说法正确的是
A.两个容器内气体的压强相等 B.两个容器内O2比O3的质量小
C.两种气体所含的质子数目相等 D.两种气体的分子数目相等
2. 甲、乙两烧杯溶液中,含有大量的Cu2+、Na+、H+、SO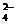 、CO
、CO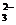 、OH-等6种离子。已知甲烧杯的溶液显蓝色,则乙烧杯的溶液中大量存在的离子是
、OH-等6种离子。已知甲烧杯的溶液显蓝色,则乙烧杯的溶液中大量存在的离子是
A.Cu2+、H+、SO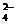 B.CO
B.CO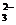 、OH-、SO
、OH-、SO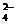
C.Na+、OH-、CO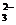 D. Na+、H+、SO
D. Na+、H+、SO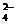
1.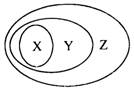 右图表示的一些物质或概念间的从属关系中不正确的是
右图表示的一些物质或概念间的从属关系中不正确的是
|
|
X |
Y |
Z |
|
A |
苯的同系物 |
芳香烃 |
芳香族化合物 |
|
B |
胶体 |
分散系 |
混合物 |
|
C |
电解质 |
离子化合物 |
化合物 |
|
D |
碱性氧化物 |
金属氧化物 |
氧化物 |
21.(本题满分14分)
已知数列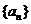 中,
中,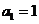 ,且
,且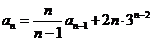
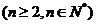 .
.
(Ⅰ) 求数列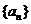 的通项公式;
的通项公式;
(Ⅱ) 令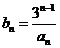
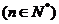 ,数列
,数列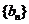 的前
的前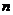 项和为
项和为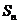 ,试比较
,试比较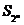 与
与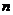 的大小;
的大小;
(Ⅲ) 令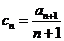
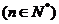 ,数列
,数列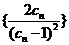 的前
的前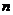 项和为
项和为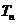 ,求证:对任意
,求证:对任意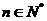 ,
,
都有 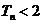 .
.
21解:(Ⅰ)由题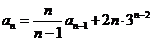 知,
知, 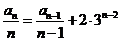 ,
,
由累加法,当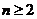 时,
时,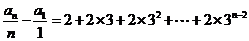
代入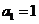 得,
得,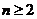 时,
时,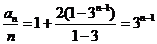
又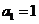 ,故
,故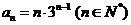 .
................4分
.
................4分
(II)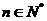 时,
时,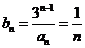 ,则
,则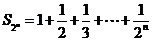
记函数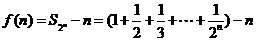
所以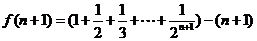 .........6分
.........6分
则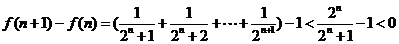
所以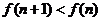 .
.
由于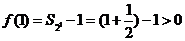 ,此时
,此时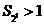 ;
;
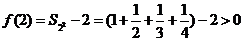 ,此时
,此时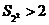 ;
;
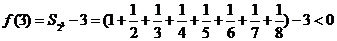 ,此时
,此时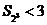 ;
;
由于,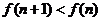 ,故
,故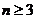 时,
时,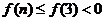 ,此时
,此时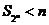 .
.
综上所述:当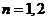 时,
时,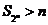 ;当
;当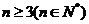 时,
时,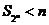 . ...........10分
. ...........10分
(III)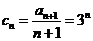
当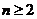 时,
时,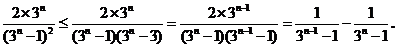
所以当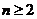 时,
时,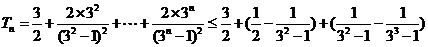
+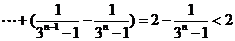 .
.
且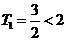
故对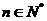 ,
,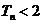 得证.
.................14分
得证.
.................14分
20.(本题满分13分)
已知函数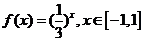 ,函数
,函数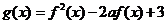 的最小值为
的最小值为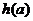 .
.
(1)求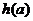 的解析式;
的解析式;
(2)是否存在实数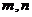 同时满足下列两个条件:①
同时满足下列两个条件:①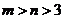 ;②当
;②当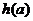 的定义域为
的定义域为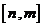 时,值域为
时,值域为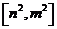 ?若存在,求出
?若存在,求出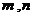 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
20解:(1)由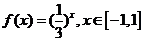 ,知
,知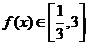 ,令
,令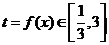
............1分
记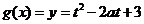 ,则
,则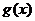 的对称轴为
的对称轴为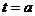 ,故有:
,故有:
①当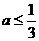 时,
时,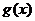 的最小值
的最小值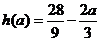
②当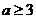 时,
时,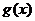 的最小值
的最小值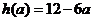
③当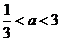 时,
时,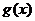 的最小值
的最小值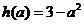
综述,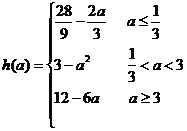 ............7分
............7分
(2)当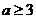 时,
时,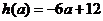 .故
.故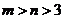 时,
时,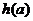 在
在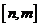 上为减函数.
上为减函数.
所以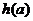 在
在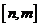 上的值域为
上的值域为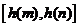 .
............9分
.
............9分
由题,则有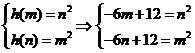 ,两式相减得
,两式相减得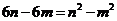 ,又
,又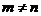
所以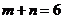 ,这与
,这与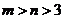 矛盾.故不存在满足题中条件的
矛盾.故不存在满足题中条件的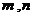 的值.
的值.
............13分
19.(本题满分12分)
已知二次函数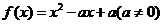 ,不等式
,不等式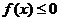 的解集有且只有一个元素,设数列
的解集有且只有一个元素,设数列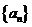 的前
的前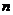 项和为
项和为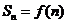 .
.
(1)求数列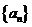 的通项公式;
的通项公式;
(2)设各项均不为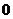 的数列
的数列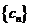 中,满足
中,满足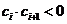 的正整数
的正整数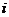 的个数称作数列
的个数称作数列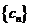 的变号数,令
的变号数,令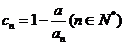 ,求数列
,求数列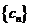 的变号数.
的变号数.
19解:(1)由于不等式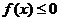 的解集有且只有一个元素,
的解集有且只有一个元素,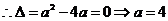
故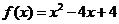 .
..................2分
.
..................2分
由题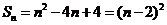
则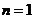 时,
时,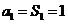 ;
;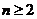 时,
时,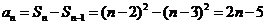
故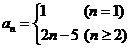 ...................6分
...................6分
(2)由题可得,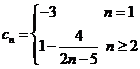 ,
,
由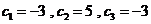 ,所以
,所以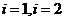 都满足
都满足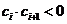 ..............8分
..............8分
当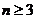 时,
时,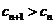 ,且
,且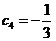 ,同时
,同时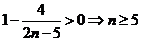 ,可知
,可知
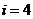 满足
满足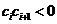 ;
;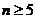 时,均有
时,均有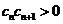 .
.
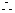 满足
满足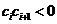 的正整数
的正整数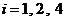 ,故数列
,故数列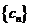 的变号数
的变号数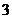 . ............12分
. ............12分
18.(本题满分12分)
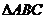
 中,角
中,角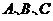 的对边分别为
的对边分别为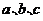 ,且
,且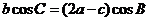 .
.
(1)求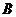 的大小;
的大小;
(2)若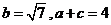 ,求
,求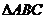 的面积.
的面积.
18解:(1)由正弦定理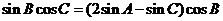 ,
,
即有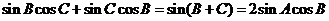 .
.
由于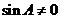 ,知
,知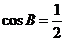 ,且
,且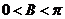 ,故
,故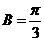 . ..............6分
. ..............6分
(2)由于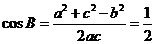 ,代入
,代入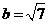 ,
,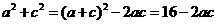
得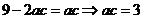 ,所以
,所以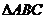 的面积
的面积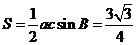 .
.......12分
.
.......12分
17.(本题满分12分)
已知函数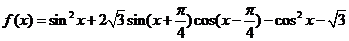 .
.
(1)求函数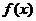 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)求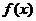 在
在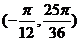 上的值域.
上的值域.
17解:(1)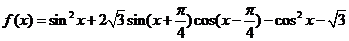
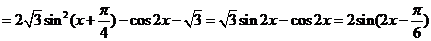
..............3分
故函数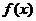 的最小正周期
的最小正周期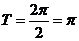
令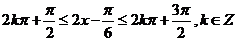 ,得
,得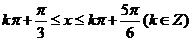
故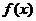 的单调递减区间为
的单调递减区间为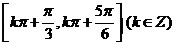 .
..............6分
.
..............6分
(2)当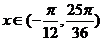 ,知
,知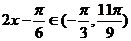 ,故
,故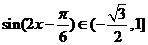 .
.
所以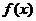 在
在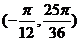 上的值域是
上的值域是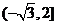 .
..............12分
.
..............12分
16.(本题满分12分)
已知关于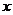 的方程
的方程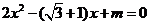 的两根为
的两根为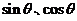 ,其中
,其中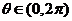 .
.
(1)求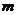 的值;
的值;
(2)求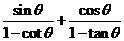 的值.
的值.
16解:(1)由根与系数的关系知,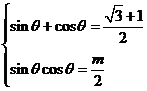
又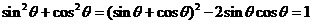 ,
,
知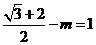 ,求得
,求得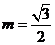 .
..............6分
.
..............6分
(2)由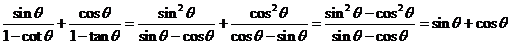
故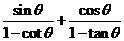 的值为
的值为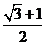 .
..............12分
.
..............12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com